Plano inclinado com atrito

Plano inclinado com atrito Exercícios

01-(UERJ-RJ) Um bloco de massa igual a 1,0 kg repousa em equilíbrio sobre um plano inclinado. Esse plano tem comprimento igual a 50 cm e alcança uma altura máxima em relação ao solo igual a 30 cm. Calcule o coeficiente de atrito entre o bloco e o plano inclinado.

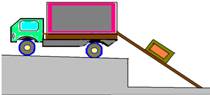
02-(UFPEL) Um caminhão-tanque, após sair do posto, segue, com velocidade constante, por uma rua plana que, num dado trecho, é plana e inclinada.

 O módulo da aceleração da gravidade, no local, é g=10m/s², e a massa do caminhão, 22t, sem considerar a do combustível.

É correto afirmar que o coeficiente de atrito dinâmico entre o caminhão e a rua é

03-(Ufrrj-RJ) Um bloco se apóia sobre um plano inclinado, conforme representado no esquema:

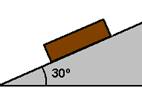
Dados: sen 30° = 0,5

Se o bloco tem peso de 700N, a menor força de atrito capaz de manter o bloco em equilíbrio sobre o plano é

a) 350N.               b) 300N.               c) 250N.               d) 200N.               e) 150N.

04-(UNIFESP-SP) Conforme noticiou um site da Internet em 30.8.2006, cientistas da Universidade de Berkeley, Estados Unidos, "criaram uma malha de microfibras sintéticas que utilizam um efeito de altíssima fricção para sustentar cargas em superfícies lisas", à semelhança dos "incríveis pêlos das patas das lagartixas".

            ("www.inovacaotecnologica.com.br").

Segundo esse site, os pesquisadores demonstraram que a malha criada "consegue suportar uma moeda sobre uma superfície de vidro inclinada a até 80°" (veja a foto).

Dados sen 80° = 0,98; cos 80° = 0,17 e tg 80° = 5,7, pode-se afirmar que, nessa situação, o módulo da força de atrito estático máxima entre essa malha, que reveste a face de apoio da moeda, e o vidro, em relação ao módulo do peso da moeda, equivale a, aproximadamente,

a) 5,7%.               b) 11%.                c) 17%.                d) 57%.                e) 98%.

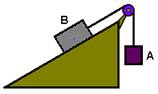
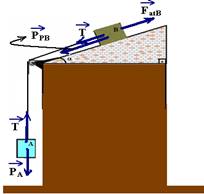
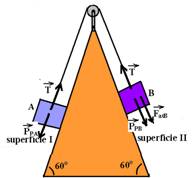
05-(IME-RJ) No plano inclinado da figura, os corpos A e B, cujos pesos são de 200N e 400N, respectivamente, estão ligados por um fio que passa por uma polia lisa.

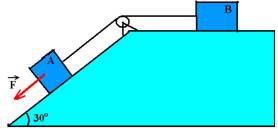
O coeficiente de atrito entre os corpos e o plano é 0,25. Determine a intensidade da força 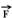 de modo que o movimento se torne iminente. Considere g=10m/s², cos30^o=0,87 e sen30^o=0,5.

06-(UFB) Um corpo de massa 1kg, partindo do repouso em A, desce o plano inclinado AB e, em seguida desliza na superfície plana e horizontal BC, parando em C, após percorrer 4 m nessa superfície. O coeficiente de atrito entre o corpo e as duas superfícies é o mesmo e vale 0,2.

Considere cosq=0,8, senq=0,6, g=10m/s² e determine:

a) a reação do plano inclinado.

b) a variação de velocidade entre as posições inicial e final.

c) a intensidade da força de atrito nos planos AB e BC.

d) a aceleração no plano horizontal

e) a velocidade máxima atingida pelo móvel

f) a distância percorrida no plano inclinado

07-(FUVEST-SP) Um plano inclinado liso faz um ângulo de 30^o em relação a um plano horizontal áspero.

Um corpo de massa 10kg, abandonado no plano inclinado, demora 2s para atingir o plano horizontal. Determine: (g=10m/s²)

a) a distância percorrida pelo móvel no plano inclinado

b) a distância percorrida no plano horizontal, sabendo que o coeficiente de atrito entre o corpo e o plano horizontal é igual a 0,2.

08-(PUC-SP) Um caixote de madeira de 4,0 kg é empurrado por uma força constante 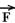e sobe com velocidade constante de 6,0 m/s um plano inclinado de um ângulo a, conforme representado na figura.

A direção da força 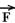 é paralela ao plano inclinado e o coeficiente de atrito cinético entre as superfícies em contato é igual a 0,5. Com base nisso, analise as seguintes afirmações: (g=10m/s²)

I) O módulo de 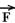 é igual a 24 N.

II) 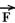 é a força resultante do movimento na direção paralela ao plano inclinado.

III) As forças contrárias ao movimento de subida do caixote totalizam 40 N.

IV) O módulo da força de atrito que atua no caixote é igual a 16 N.

Dessas afirmações, é correto apenas o que se lê em

a) I e II                    b) I e III                     c) II e III                     d) II e IV                      e) III e IV

09- (Mackenzie-SP) A ilustração refere-se a certa tarefa na qual o bloco B, dez vezes mais pesado que o bloco A, deverá descer pelo plano inclinado com velocidade constante.

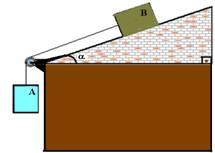
Considerando que o fio e a polia são ideais, o coeficiente de atrito cinético entre o bloco B e o plano deverá ser:

(Dados: sena =0,6  e  cosa = 0,8)

a) 1,50                     b) 1,33                     c) 0,875                     d) 0,750                     e) 0,500

10-(ITA-SP) Um pequeno bloco de madeira de massa m = 2 kg encontra-se sobre um plano inclinado que está fixo no chão, como mostra a figura. Com que força F devemos pressionar o corpo sobre o plano para que o mesmo permaneça em repouso?

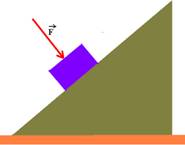
Dados: Coeficiente de atrito estático entre o bloco e o plano inclinado, m=0,4; comprimento do plano inclinado=1m; altura do plano inclinado=0,6m e aceleração da gravidade local=9,8m?s².

a) 13,7N                    b) 15,0N                    c) 17,5N                     d) 11,2N                       e) 10,7N 

11-(UNESP-SP) Um bloco de massa 5,0kg está apoiado sobre um plano inclinado de 30° em relação a um plano horizontal.

Se uma força constante, de intensidade F, paralela ao plano inclinado e dirigida para cima, é aplicada ao bloco, este adquire uma aceleração para baixo e sua velocidade escalar é dada por v = 2,0t (SI), (fig.1). Se uma força constante, de mesma intensidade F, paralela ao plano inclinado e dirigida para baixo for aplicada ao bloco, este adquire uma aceleração para baixo e sua velocidade escalar é dada por v' = 3,0t (SI), (fig. 2).

                               

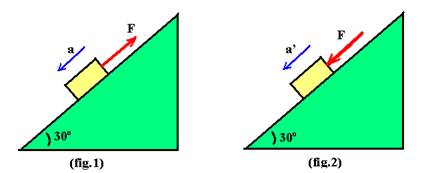
  a) Calcule F, adotando g = 10m/s².

  b) Calcule o coeficiente de atrito de deslizamento entre o corpo e o plano inclinado.

12-(CESGRANRIO) Um corpo de massa m = 0,20kg desce um plano inclinado de 30° em relação à horizontal. O gráfico apresentado mostra como varia a velocidade escalar do corpo com o tempo.

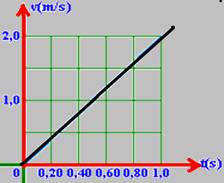
 a) determine o módulo da aceleração do corpo;

 b) calcule a intensidade da força de atrito do corpo com o plano. Dados: g = 10m/s², sen 30° = 0,50, cos 30° = 0,87.

13-(PUC-PR) Os corpos A e B de massas mA e mB, respectivamente, estão interligados por um fio que passa pela polia, conforme a figura. A polia pode girar livremente em torno de seu eixo. A massa do fio e da polia são considerados desprezíveis.

Se o sistema está em repouso é correto afirmar:

I. Se m_A = m_B, necessariamente existe atrito entre o corpo B e o plano inclinado.

II. Independente de existir ou não atrito entre o plano e o corpo B, deve-se ter m_A = m_B.

III. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente m_A > m_B.

IV. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente m_B > m_A.

Está correta ou estão corretas:

a) Somente I.          b) Somente II .          c) I e III.          d) I e IV.           e) Somente III.

14-(UFPel-RS) Uma empresa de transportes faz a entrega de produtos para um supermercado. Um desses produtos é de dimensões consideráveis e peso elevado, o que requer o uso de uma máquina simples (plano inclinado) para facilitar a descarga.

Suponha que a inclinação do plano de apoio, em relação à horizontal, não seja suficiente para provocar o deslizamento da caixa rampa abaixo. Resolva, para a situação proposta, as questões que se seguem:

a) Represente graficamente as forças que atuam sobre a caixa.

b) Qual é a intensidade da força resultante na direção do plano de apoio? Justifique.

c) qual é o valor do coeficiente de atrito entre a caixa e o plano, considerando, para esse caso, que a inclinação do plano de apoio, igual a 30^o, é máxima, sem que a caixa deslize? Dados: sen30^o=0,5; cos30^o=0,87).

15-(Olimpíada Brasileira de Física) Um bloco desliza sobre um plano inclinado com atrito (ver figura).

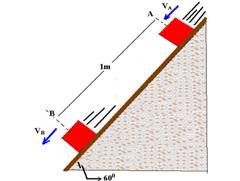
No ponto A, a velocidade é V_A=2m/s, e no ponto B, distante 1m do ponto A ao longo do plano, V_B=3m/s. Considere sen60^o=Ö3/2; cos60^o=1/2 e g=10m/s²) e obtenha o valor do coeficiente de atrito cinético entre o bloco e o plano.

a) Ö3                   b) Ö3/2                     c) Ö3/2 + 1                      d) Ö3 + ½                       e) Ö3 – ½

16-(UNESP-SP) Ao modificar o estilo se uma casa para o colonial, deseja-se fazer a troca do modelo de telhas existentes. Com o intuito de preservar o jardim, foi montada uma rampa de 10m de comprimento, apoiada na beirada do madeiramento do telhado, a 6m de altura.

 No momento em que uma telha --- que tem massa de 2,5kg --- é colocada sobre a rampa, ela desce acelerada, sofrendo, no entanto, a ação do atrito. Nessas condições, determine o valor da aceleração desenvolvida pela telha. Dado: coeficiente de atritom=0,2;g=10m/s²).

17-(MACKENZIE-SP) Os corpos A e B da figura são idênticos e estão ligados por meio de um fio suposto ideal. A polia possui inércia desprezível, a superfície I é altamente polida e o coeficiente de atrito cinético entre a superfície II e o corpo B é m=0,2. Considere g=10m/s².

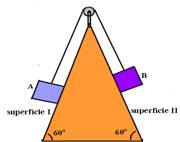
Em determinado instante, o corpo A está descendo com velocidade escalar de 3m/s. Calcule sua velocidade escalar após 2s.

18-(UFG) Um catador de recicláveis de massa m sobe uma ladeira puxando seu carrinho. O coeficiente de atrito estático entre o piso e os seus sapatos é m_e e o ângulo que a ladeira forma com a horizontal e q. O carrinho, por estar sobre rodas, pode ser considerado livre de atrito. A maior massa do carrinho com os recicláveis que ele pode suportar, sem escorregar, e de:

19-(ITA-SP) A partir do nível P, com velocidade inicial de 5 m/s, um corpo sobe a superfície de um plano inclinado PQ de 0,8 m de comprimento. Sabe-se que o coeficiente de atrito cinético entre o plano e o corpo é igual a 1/3.

Considere a aceleração da gravidade g = 10 m/s2, sen q = 0,8, cos q = 0,6 e que o ar não oferece resistência. O tempo mínimo de percurso do corpo para que se torne nulo o componente vertical de sua velocidade é

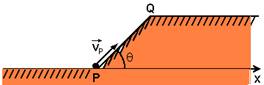
a) 0,20 s.                    b) 0,24 s.                      c) 0,40 s.                       --d) 0,44 s.                      e) 0,48 s.

20-(Ufrrj-RJ) Um homem puxa uma caixa de massa 2 kg para cima de um plano inclinado de um ângulo 30° em relação à horizontal, por meio de um fio ideal, que faz um ângulo também de 30° com o plano, conforme mostra a figura. O coeficiente de atrito entre a caixa e o plano é m = 0,2.(g=10m/s²)

21-(FUVEST) - Um bloco de massa m, montado sobre rodas (para tornar o atrito desprezível), parte do repouso em A e leva um tempo t para atingir B. A massa das rodas é desprezível. Retirando-se as rodas, verifica-se que o bloco, partindo do repouso em A, leva um tempo 2t para atingir B. A alturas entre A e o solo é h.

 a) Determinar o valor de t.

 b) Determinar o valor do coeficiente de atrito entre o plano e o bloco sem rodas, em função de a.

22-(MACKENZIE-SP-009)  Certo corpo começa a deslizar, em linha reta, por um plano inclinado, a partir do repouso na posição x_o= 0. Sabendo-se que após 1,00 s de movimento, ele passa pela posição x₁ = 1,00 m e que, com mais 3,00 s, ele chega à posição x₂, o coeficiente de atrito cinético entre as superfícies em contato (μ_c) e a posição x₂ são, respectivamente, iguais a:

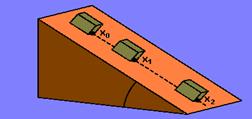
Dados  ---  sen β = 0,6  ---  cos β = 0,8  ---  g = 10m/s²

a)  0,25 e 16,00 m         b)  0,50 e 8,00 m         c)  0,25 e 8,00 m         d)  0,50 e 16,00 m         e)  0,20 e 16,00 m 

23-(PUC-RJ-010)  Um bloco escorrega a partir do repouso por um plano inclinado que faz um ângulo de 45º com a horizontal. Sabendo que durante a queda a aceleração do bloco é de 5,0 m/s² e considerando g= 10m/s², podemos dizer que o coeficiente de atrito cinético entre o bloco e o plano é

a) 0,1                                     b) 0,2                                      c) 0,3                                     d) 0,4                                        e) 0,5 

24-(UERJ-RJ-011) A figura abaixo representa o plano inclinado ABFE, inserido em um paralelepípedo retângulo ABCDEFGH de base horizontal, com 6 m de altura CF, 8 m de comprimento BC e 15 m de largura AB, em repouso, apoiado no solo.

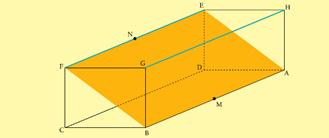
Admita um  corpo de massa igual a 20 kg que desliza com atrito, em movimento retilíneo, do ponto F ao ponto B, com velocidade constante. A força de atrito, em newtons, entre a superfície deste corpo e o plano inclinado é cerca de:

a) 50                                           b) 100                                                     c) 120                                                 d) 200

25-(UPE-PE-011) Um bloco de aço é colocado sobre uma tábua de apoio que vai se inclinando aos poucos. Quando o bloco fica na iminência de escorregar, a tábua forma com a horizontal um ângulo β de acordo com a figura a seguir:

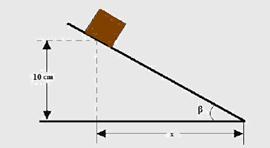
Sabendo-se que o coeficiente de atrito estático entre o bloco e a tábua vale μ_e=0,40 é correto afirmar que a distância x indicada na figura, em centímetros, vale:

a) 25                                b) 10                                          c) 12                                     d) 20                                            e) 4

26-(UFRJ-RJ-011) Um bloco de massa 2,0 kg está sobre a superfície de um plano inclinado, que está em movimento retilíneo para a direita, com aceleração de 2,0 m/s², também para a direita, como indica a figura a seguir. A inclinação do plano é de 30^o em

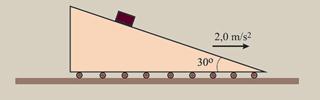
relação à horizontal. Suponha que o bloco não deslize sobre o plano inclinado e que a aceleração da gravidade seja g = 10 m/s².

Usando a aproximação √3≈1,7, calcule o módulo e indique a direção e o sentido da força de atrito exercida pelo plano inclinado sobre o bloco.

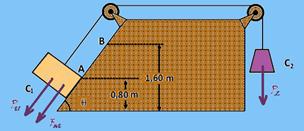
27-(MACKENZIE-SP-011) Com relação à rampa de apoio, os corpos C₁ e C₂ estão em repouso e na iminência de movimento. Ao abandonar-se o conjunto, o corpo C₁ sobe a rampa, com a qual existe atrito cinético de coeficiente μ = 0,2. Considerando-se os

dados da tabela abaixo e fios e polias ideais, o ganho de energia cinética do

  

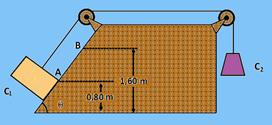
corpo C₂, durante o deslocamento do corpo C₁, do ponto A ao ponto B, é de

a) 20 J                       b) 2,0 J                                c) 1,6 J                              ---d) 0,80 J                         e) 0,60 J

28-(USS-RJ-011) Uma pequena esfera de massa m é abandonada em repouso no ponto A de um plano inclinado sem atrito, AC.

 altura do plano é AB=12 metros. A partir do ponto C, a esfera passa a se mover sobre a superfície horizontal com atrito, e pára em

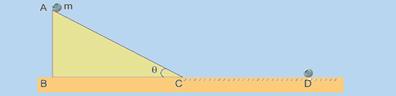
D, tal que CD=20 metros. O coeficiente de atrito dinâmico entre a esfera e a superfície horizontal vale:

a)0,16                   b)0,25                          c)0,30                                      d)0,48                                 e)0,60

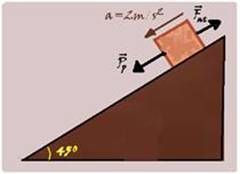
29-(UECE-CE-012)

Um bloco, sob ação da gravidade, desce um plano inclinado com aceleração de 2 m/s². Considere o módulo da

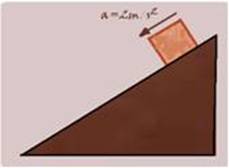
aceleração da gravidade g=10 m/s². Sabendo-se que o ângulo de inclinação do plano é 45^o com a horizontal, o coeficiente de atrito cinético entre o bloco e o plano é, aproximadamente,

A) 0,7.                    B) 0,3.                          C) 0,5.                             D) 0,9.

30-(UFPE-PE-012)

Um bloco de massa m = 4,0 kg é impulsionado sobre um plano inclinado com velocidade inicial v_o = 15 m/s, como

mostra a figura. Ele desliza em um movimento descendente por uma distância L = 5,0 m, até parar. Calcule o módulo da força resultante que atua no bloco, ao longo da descida, em newtons.

31-(UEPA-PA-012)

Num parque de diversões há um escorregador infantil, conforme indica a figura abaixo.

Neste brinquedo, as crianças, inicialmente em repouso, partem do ponto A e atingem o ponto B. Suponha que o coeficiente de atrito entre as superfícies de contato seja igual a 0,5.

Considerando que, quando uma criança escorrega, a dissipação de energia ocorra apenas pela ação da força de atrito, e sabendo que  a  ingestão de um sorvete fornece 112.000 J, o número de vezes que uma criança de 20 kg deverá escorregar pelo brinquedo para perder a energia correspondente à ingestão de um sorvete é:

Dados: g = 10 m/s2; sen 45° = cos 45° = 0,7 

a) 100                             b) 200                               c) 300                              d) 400                                e) 500

Resoluções

01-O plano inclinado possui uma secção transversal que é um triângulo retângulo de hipotenusa 50 cm e cateto 30 cm. O outro cateto, por Pitágoras, deve ser de 40 cm.

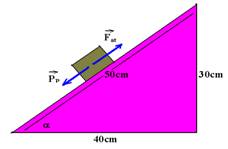
sena=cateto oposto/hipotenusa=30/50  ---  sena=0,6        cosa=cateto adjacente/hipotenusa=40/50  ---  cosa=0,8

Como o bloco está em equilíbrio a força resultante sobre ele é nula e assim, PP=Fat  ---  mgsena=mmgcosa  ---  0,6=m.0,8  --- 

m=0,75

02- Como ele está com velocidade constante a força resultante sobre ele é nula e, nesse caso Fat=PP. Seja M a massa total (caminhão + combustível)  ---  mMgcosa=Mgsena  ---  m=sena/cosa=tga  ---  R- D

03- A menor força de atrito para mantê-lo em equilíbrio vale F_at=P_P=Psen30^o=700.0,5  ---  F_at=350N  R-A

04- Esquema:

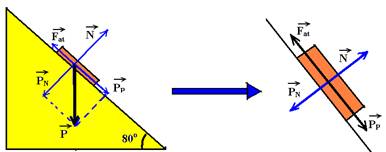
P_P=Psen80^o=P.0,98 ---  no equilíbrio – F_at=P_P  ---  F_at=P.0,98  ---  F_at/P=0,98  ---  0,98=98/100  ---  98%  R-E

05- Colocando as forças na direção do movimento.

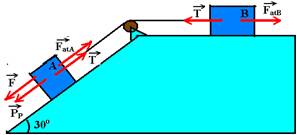
P_P=P_Asen30^o=200.0,5  ---  P_P=100N  ---  F_atA=mP_Acos30^o=0,25.200.0,87  ---  F_atA=43,5N  ---  F_atB=mN=mP_B=0,25.400  ---  F_atB=100N

Na iminência de movimento a intensidade da força resultante sobre cada bloco é nula  ---  bloco B – T=F_atB  ---  T=100N  --- 

bloco A –  F + P_P=F_atA + T  ---  F + 100=43,5 + 100  ---  F=43,5N

06- a) A reação do plano inclinado é N=P_N=Pcosq=mgcosq=1.10.0,8  ---  P_N=8N

b) A velocidade inicial é nula (partiu do repouso) e a final também (parou). Assim, DV=0

c) No plano inclinado AB  ---  F_at=mN_i  ---  F_ati=mP_N=0,2.8  ---  F_at=1,6N

    No plano horizontal BC  ---  F_at=mN_h=mP=0,2.10  ---  F_at=2N

d) No plano horizontal a força resultante sobre ele é a força de atrito horizontal que o obriga a parar em C, ou seja, F_R=F_at

F_R=ma=F_at  ---  F_at=ma  ---  2=1a  ---  a=2m/s²

e) Ele parte do repouso em A, desce acelerando e atinge a velocidade máxima em B (V­_B)

Torricelli  ---  V_C²=V_B² + 2.a.DS  ---  0²=V_B² + 2.(-2).4  ---  V_B=4m/s

f) Colocando as forças que agem sobre o corpo, na direção do movimento, em sua descida pelo plano inclinado

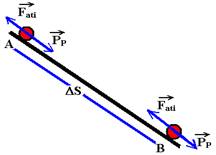
F_at=1,6N  ---  P_P=Psenq=10.0,6  ---  P_P=6N  ---  F_R=ma  ---  P_P – F_ati=ma  ---  6 – 1,6=1.a  ---  a=4,4m/s²

Torricelli  ---  V_B²=V_A² + 2.a.DS  ---  4²=0² + 2.4,4.DS  ---  DS»1,8m

07- a) Como no plano inclinado não existe atrito a força resultante sobre o corpo é o P_P  ---  F_R= P_P=ma  ---  mgsen30^o=ma  --- 

10.10.0,5=10.a  ---  a=5m/s²  ---  DS=V_o.t + a.t²/2  ---  DS=0.2 + 5.2²/2  ---  DS=10m

b) Cálculo da velocidade V_p com que o corpo chega à base do plano inclinado  ---  V_p=V_o + at  ---  V_p=0 + 5.2  ---  V_p=10m/s

No plano horizontal existe atrito e a força resultante é o próprio F_at 

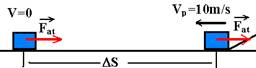
F_R=F_at=m.a  ---  mN=m.a  ---  mP=ma  ---  0,2.100=10.a  ---  a=2m/s²

Torricelli  ---  V² = V_p² + 2.a.DS  ---  0² = 10² + 2.(-2).DS  ---  DS=25m

08- Forças que agem sobre o bloco na direção do movimento:

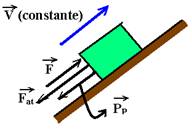
F_at=mmgcosa=0,5.4.10.0,8  ---  F_at=16N  ---  P_P=mgsena=4.10.0,6  ---  P_P=24N  ---  no equilíbrio dinâmico  ---  F_R=0  --- 

F=P_P + F_at  ---  F=24 + 16  ---  F=40N

R- E

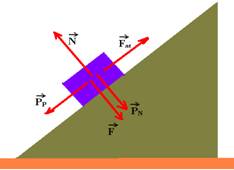
09- Como g é o mesmo (mesmo focal), se P_B=10P_A  ---  m_B=10m_A.

Colocando as forças

Como está com velocidade constante está em equilíbrio dinâmico e a força resultante sobre cada bloco é nula  ---  bloco A  --- 

T=P_A  ---  T=m_Ag   ---  bloco B  ---  F_atB=P_PB + T  ---  mm_Bgcosa = m_Bgsena + m_Ag  --- m10m_Agcosa =10m_Agsena + m_Ag  ---  m.10.0,8=10.0,6 + 1  ---  8m=1,6  ---  m=0,875 R- C 

10- Colocando as forças:

sena=0,6/1  ---  sena=0,6  ---  cosa=0,8/1  ---  cosa=0,8  ---  como ele está em repouso a força resultante sobre ele é nula, então  ---   P_P=F_at  ---  mgsena = mN  ---  mgsena =m(P_N + F)  ---  mgsena = m(mgcosa + F)  ---  2.9,8.0,6 = 0,4.(2.9,8.0,8 + F)  --- 

11,76 = 6,272 + 0,4F  ---  F=5,488/0,4  ---  F=13,72N  R- A

11- P_P e F_at são os mesmos tanto na figura 1 como na figura 2

 a) figura 1  ---  P_P=mgsen30^o=5.10.0,5  ---  P_P=25N  ---  comparando V=V_o + a.t com V=2,0.t, concluímos que V_o=0 e a=2m/s²

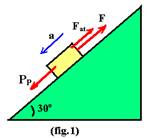
F_R=ma  ---  P_P – F –F_at=ma  ---  25 – F – F_at=5.2  ---  F + F_at=15 I 

Figura 2  ---  P_P=25N  ---  comparando V=V_o + a’.t com V=3,0.t, concluímos que V_o=0 e a’=3m/s² 

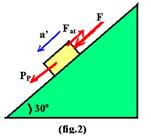
F_R=ma’  ---  P_P + F – F_at=ma’  ---  25 + F – F_at=5.3  ---  F=F_at – 10 II  ---  II em I  ---  F_at– 10 + F_at=15  ---  F_at=12,5N  ---  F + F_at=15  ---  F + 12,5 = 15  ---  F=2,5N

b) F_at=mmgcos30^o  ---  12,5=m.5.10.Ö3/2  ---  m=12,5/25Ö3  ---  m»0,3

12- a)Cálculo da aceleração pelo gráfico  ---  a=DV/Dt=2,0/1,0  ---  a=2m/s²

b) F_R=ma ---  P_P – F_at=ma  ---  mgse30^o – F_at = m.a  ---  0,2.10.0,5 – F_at=0,2.2  --- F_at=0,6N

13-  I- Correta, pois P_PB é sempre menor que P_A.      II- Falsa, vide I.      III- Não necessariamente, pois F_atB de dos valores do coeficiente de atrito m e do ângulo de inclinação do plano.      IV- Correta, vide I.   R- D

14-

a)

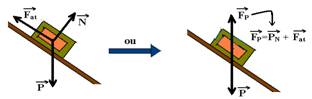
b) Na direção do plano de apoio as forças que agem sobre a caixa são:

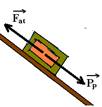
Como a caixa está em repouso, a força resultante sobre ela é nula  ---  

c) P_P=F_at  ---  mgsen30^o=mmgcos30^o  ---  0,5=m0,87  ---  m»0,57

15- Cálculo da aceleração  ---  Torricelli  ---  V_B²=V_A² + 2.a.DS  ---  9=4 +2.a.1  --- a=2,5m/s²  ---  F_R=ma  ---  P_P – F_at=m.a  --- 

mgsen60^o - mmgcos60^o=m.a  ---  10.Ö3/2 - m.10.0,5=2,5  ---  5Ö3 - 5m=2,5  ---  m=Ö3 – 1/2   R- E

16- As forças que agem sobre a telha são P_P e F_at:

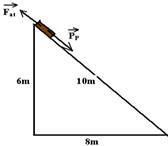
Se a hipotenusa é 10 e um cateto é 6, aplicando Pitágoras, o outro cateto é 8  ---  sena=6/10=0,6  ---  cosa=8/10=0,8  ---  F_R=ma  ---  P_P – F_at=ma  ---  mgsena -mmgcosa=ma  ---  10.0,6 – 0.2.10.0,8=a  ---  a=4,4m/s²

17- Colocando as forças:

Como o bloco A está descendo, B está subindo e o F_at nele é para baixo  ---  bloco A – não tem atrito  – F_R=ma  ---  P_PA – T=ma  ---  mgsen60^o - T=ma  ---  Ö3/2mg – T=ma I  ---  bloco B – tem atrito  ---  T – P_PB – F_atB=ma  ---  T – mgsen60^o - mmgcos60^o=ma  --  T - mgÖ3/2 – 0,2.m.g.0,5=ma II  ---  somando membro a membro I com II   ---  -0,1m=2ma  ---  a=-0,5m/s²  ---  V=Vo +a.t  --- 

V=3 – 0,5.2  ---  V=2m/s

18-Colocando as forças

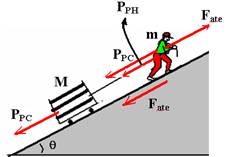
Sobre o homem agem as forças  ---  F_ate=mN  ---  F_ate=mP_N  ---  F_ate=mmgcosq  - força de atrito estático máximo que ele troca com o plano inclinado e que é responsável por ele subir sem escorregar  ---  P_PC=Mgsenq - força com que ele puxa o carrinho de massa M através do fio ---  P_PH=mgsenq   ---  parcela de seu peso de massa m, que ele deve vencer

F_ate=P_Pc + P_PH  ---  mmgcosq=Mgcosq + mgsenq  ---  M=m(mcosq - senq)/senq  ---  M=m(mcosq/senq - senq/senq)  --- 

M=m(mcosq/senq - 1) R- E

19-Cálculo da velocidade com que o corpo chega ao ponto Q. No trecho PQ as forças que agem sobre o corpo na subida são P_P e F_at.

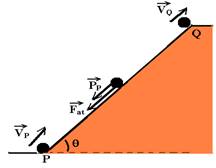
P_P=mgsenq=m.10.0,8  ---  P_P=8m  ---  F_at=mmgcosq=1/3.m.10.0,6  ---  F_at=2m  ---  F_R=ma  ---  P_P + F_at=ma  ---  8m + 2m=ma  ---  a=10m/s²  ---  cálculo da velocidade com que chega em Q  ---  Torricelli  ---  V_Q² = V_P² + 2.a.DS  ---  V_Q²=25 + 2.(-10).0,8  --- 

V_Q=3m/s  ---  cálculo do tempo que demora para chegar em Q  ---  V_Q=V_P + a.t  ---  3=5 + (-10).t  ---  t=0,2s

A partir de Q, aonde chega com velocidade de 3m/s, ocorre um lançamento oblíquo com ângulo de lançamento q.

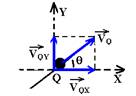
Como o exercício quer o instante em que a componente vertical da velocidade se anula, vamos trabalhar apenas com ela (eixo Y).

Decompondo V_Q no eixo vertical Y  ---  V_QY=V_Qsenq   ---  V_QY=3.0,68  ---  V_QY=2,4m/s   ---  quando a componente vertical da velocidade se anula, V_Y=0  ---  V_Y=V_o + g.t  ---  0=2,4 + (-10).t  ---  t=0,24s  ---  t_t=0,2 + 0,24  ---  t_t=0,44s

20-a) As forças que agem sobre a caixa são:

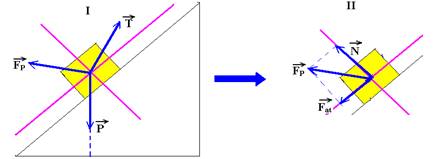
figura I  ---  - peso, vertical e para baixo exercida pela Terra  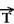---   - força de tração, exercida pelo fio  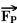---   - força exercida pelo plano.

Figura II – a força exercida pelo plano 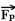 é a soma vetorial da força normal 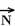com a força de atrito 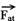, ou seja,  =  + .

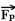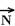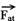b) Decompondo as forças nos eixos X e Y

T_X=Tcos30^o  ---  T_X=TÖ3/2  ---  T_Y=Tsen30^o  ---  T_Y=T/2  ---  P_X=mgsen30^o  --- P_X=mg/2  ---  P_Y=mgcos30^o  ---  P_Y=mgÖ3/2

F_at=mN

Equilíbrio na direção X  ---  T_X=P_X + F_at  ---  TÖ3/2=mg/2 + mN  I    ----    equilíbrio na direção Y  ---  N + T_Y=P_Y  --- 

N=mgÖ3/2 – T/2 II  ---  II em I  ---  TÖ3/2=mg/2 + m(mgÖ3/2 – T/2)  ---  T(Ö3 + m)=mg(1 + mÖ3)  ---  T= mg(1 + mÖ3)/ (Ö3 + m) 

Substituindo os valores  ---  T»14N

21- (a) Com rodas não existe atrito e a força resultante sobre o carrinho é P_P=F_R  ---  mgsena=ma  ---  a=gsena

DS=V_o.t + a.t²/2  ---  DS=V₀.t + gsena.t²/2 I  ---  sena=h/DS  ---  DS=h/sena II  ---  II em I  ---  h/sena=gsenat²/2  ---  t²=h/senaX

2/gsena  ---  t²=2h/g(sena)²   ---  t=(Ö2h/g) /sena

b) Sem rodas, existe força de atrito de intensidade  (F_at). Temo de descida agora é t₁=2t  ---  t₁=2(Ö2h/g) /sena

DS=V_o.t + a.t²/2  ---  h/sena=0.t + a.t₁²/2  ---  h/sena=a.4.(2h/g)/(sena)²  ---  a=2h.(sena)².g/4sena.2h  ---  a=g.sena/4 II

F_R=m.a  ---  P_P – F_at=m.a  ---  mgsena - mmgcosa=m.g(sena)/4  ---  sena - mcosa=(sena)/4  ---  mcosa=sena - (sena)/4  --- 

mcosa=(3sena)/4  ---  m=3sena/4cosa  ---  m=(3tga)/4

22- A força de atrito que atua sobre o corpo é F_at = m.m.g.cosa = 8m.m  ---   força resultante na direção do movimento  ---  F_R= m.g.sen β - 8m.m = m.a  ---  6m - 8m.m = m.a  ---   6 - 8m. = a  ---  a função horária do movimento é S = S0 + v0.t + a.t²/2  --- 

S_o = 0 e v_o = 0  ---  S = a.t²/2  ---  para t = 1 s  ---   S = 1 m  ---   1 = a.1²/2  ---  a = 2 m/s²  ---  então: 6 - 8m. = a  ---  6 - 8m. = 2  --- 8m. = 6 – 2  ---   8m. = 4  ---   m = 0,5  ---  para t = 1 + 3 = 4 s  ---  S = x₂  ---   x₂ = 2. 4²/2  ---  x₂=16m

 R- D

23- Observe ao figura abaixo onde estão colocadas todas as forças que agem sobre o bloco  ---   P_t  = P sen 45° = m g sen 45°  --

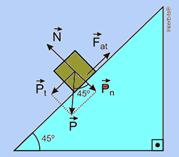
-  F_R=ma  ---   N = P_n = P cos 45° = m g cos 45°  ---  g  = 10 m/s²  ---  a = 5 m/s²  ---   q = 45°  ---   princípio fundamental da dinâmica  ---  F_R=ma  ---  P_t  – F_at = m a  ---  mgsen45^o=μmgcos45^o=ma  ---  10√2/2 – μ.10.√2/2=5  ---  m = (5√2 – 5)/5√2=

(√2 – 1)/√2=(1,4 – 1)/1,4  ---  μ≈0,3  ---  R- C

24- O corpo está em equilíbrio dinâmico (F_R=0)  ---  F_at=P_p=Psenθ  ---  senθ=FC/FB=6/10=0,6  ---  F_at=mgsenθ=20.10.0,6  ---  F_at=120N  ---  R- C

25- Na iminência de escorregar, ele está em equilíbrio e, nessas condições a parcela do peso (P_p=Psenβ) que tenta desloca-lo é equilibrada pela força de atrito (F_at)  ---  mgsenβ=μmgcosβ  ---  μ=senβ/cosβ  ---  μ=tgβ=0,40  ---  tgβ=cat. oposto/cat. adjacente  ---  0,40=10/x  ---  x=10/0,4  ---  x=25cm  ---  R- A

26- Colocando as forças que agem sobre o bloco  ---  decompondo-as na vertical e na horizontal  ---  na vertical a força

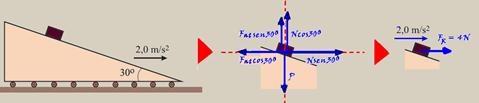
resultante é nula  --- P=F_atsen30^o + Ncos30^o  ---  20=F_at/2 + N√3/2 (I)  ---  na horizontal existe uma força resultante para a direita onde o bloco se move com aceleração a=2m/s² e de intensidade  ---  F_R=ma  ---  F_R=2.2  ---  F_R=4N  ---  F_R=N/2 – F_at.√3/2  ---

 4=N/2 – F_at.√3/2 (II)  ---  resolvendo o sistema composto por I e II e substituindo √3 por 1,7, você obterá  ---  F_at=6,6N   

27- Na figura estão colocadas as forças que agem sobre cada bloco  ---  cálculo da aceleração do sistema considerando os dois corpos como um único de massa (m₁ + m₂)=4kg  --- 

28- Trecho CD  ---  F_at=μN=μP=μmg  ---  F_at=10μm  ---  a intensidade da força resultante é a própria força de atrito  ---  F_R=ma  ---  10μm=ma  ---  a=10μ  ---  Torricelli  ---  V²=V_o²+ 2.a.ΔS  ---  0=V_o² + 2.(-a).20  ---  V_o²=2.10μ.20  ---  V_o²=400μ  --- 

 trecho AC, sem atrito, desce com aceleração a’, sujeito à P_p=mgsenθ=m.10.12/AC=120m/AC  ---  P_p=F_R=ma’  ---  120m/AC=ma’  ---  a’=120/AC  ---  Torricelli  ---  V²=V_o² + 2.a.ΔS  ---  V_o²=0² + 2.a’.AC  ---  400μ=2.120/AC.AC  ---  μ=240/400  ---  μ=0,6  ---  R- E

29-

  As forças que agem sobre o bloco na direção do movimento são  ---  P_p (parcela do peso responsável pela descida

do bloco)  ---  P_p=Psen45^o=mgsen45=m.10.√2/2=m.10.1,4/2=7m  ---  F_at (força de atrito, sempre contrária ao movimento)  ---  F_at=μ.P.sen45⁰=μ.m.g.√2/2=μ.m.10.1,4/2=7μm  ---  F_R=m.a  ---  P_p – F_at=m.a  ---  7m - 7μm=m.2  ---  μ=5/7≈0,714  ---R- A.

30-

  Durante a descida a intensidade da força resultante que age sobre o bloco é igual à intensidade da força de atrito

 

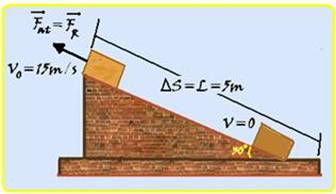
F_at=F_R ---  V_o=15m/s  ---  ∆S=L=5m  ---  para (V=0)  ---  cálculo do módulo da aceleração a pela equação de Torricelli  ---  V²=V_o² + 2.(-a).∆S  ---  0² = (15)² – 2.a.5  ---  a=22510  ---  a=22,5ms²  ---  lei fundamental da dinâmica  ---  F_R=m.a=4.22,5  ---  F_R=90N.

31-

Trata-se de um plano inclinado onde o peso do corpo, vertical e para baixo, é decomposto em duas parcelas  ---   - parcela do peso, no plano inclinado, paralela ao plano e para baixo, responsável pela descida ou tentativa de descida do bloco, de intensidade  ---

de intensidade  ---  P_P=P.senα ou P_P=mgsen α---   a energia é dissipada pela força de atrito 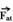  que é sempre contrária ao movimento ou à sua tendência, de intensidade  ---  F_at=μPcos45^o ou  F_at=μmgcos45^o=0,5.20.10.√2/2  ---  F_at=50√2N  ---  a força resultante, responsável pela descida do menino tem intensidade  ---  F_R=P_p – F_at=100√2 - 50√2=50√2N  ---  distância d percorrida pelo menino ao se deslocar de A para B  ---  sen45^o=2,8/d  ---  √2/2=2,8/d  ---  d=2,8√2m  ---  a energia dissipada na descida de A para B corresponde ao trabalho da força de atrito nesse trecho  ---  W_Fat=F_at.d.cos180^o (180^o é o ângulo entre o F_at e o deslocamento)  ---  W_Fat=50.√2.2.8.√2.(-1)  ---  W_Fat= - 280J (o sinal negativo significa que essa energia foi dissipada)  ---  ingestão de um sorvete  ---  W_sorvete=112.00J   ---  número de vezes que a criança deverá escorregar  ---  n=112.000/280=400 vezes  ---  R- D