Exercícios de Força de atrito

Força de atrito

01-(UFB) Considere um bloco de massa 10kg, inicialmente em repouso sobre uma superfície reta e horizontal com atrito e cujos coeficientes de atrito estático e dinâmico sejam respectivamente iguais a m_e=0,5 e m_d=0,3. Aplica-se ao bloco uma força de intensidade crescente, a partir de zero. Analise o que acontece com o bloco quando 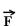tiver intensidade: (g=10m/s²)

a) F=0          b) F=20N          c) F=40N          d) F=50N          e) F=60N           f) F=35N, com o bloco em movimento

g) F=30N, com o bloco em movimento          h) Ele se move para a direita com velocidade de intensidade V, com F=0 e apenas o F_atagindo sobre ele.

02-(PUC-SP) Um bloco de borracha de massa 5,0 kg está em repouso sobre uma superfície plana e horizontal. O gráfico representa como varia a força de atrito sobre o bloco quando sobre ele atua uma força F de intensidade variável paralela à superfície.

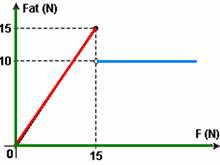
O coeficiente de atrito estático entre a borracha e a superfície, e a aceleração adquirida pelo bloco quando a intensidade da força atinge 30N são, respectivamente, iguais a

a) 0,3; 4,0 m/s²            b) 0,2; 6,0 m/s²            c) 0,3; 6,0 m/s²            d) 0,5; 4,0 m/s²            e) 0,2; 3,0 m/s²

03-(PUC-RJ) Uma caixa cuja velocidade inicial é de 10 m/s leva 5 s deslizando sobre uma superfície horizontal até parar completamente.

Considerando a aceleração da gravidade g = 10 m/s², determine o coeficiente de atrito cinético que atua entre a superfície e a caixa.

a) 0,1                     b) 0,2                     c) 0,3                      d) 0,4                     e) 0,5

04-(FUVEST-SP) Um automóvel de massa 10³kg, movendo-se inicialmente com velocidade de 72km/h é freado (em movimento uniformemente desacelerado) e pára, após percorrer 50m. Calcule a força, o tempo de freamento e o valor do coeficiente de atrito. (g=10m/s²)

05- (UFPB) Dois blocos A e B de massas m_A = 6 kg e m_B = 4 kg, respectivamente, estão apoiados sobre uma mesa horizontal e movem-se sob a ação de uma força F de módulo 60N, conforme representação na figura a seguir.

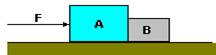
Considere que o coeficiente de atrito dinâmico entre o corpo A e a mesa é  m_A= 0,2 e que o coeficiente entre o corpo B e a mesa é  m_B = 0,3. Com base nesses dados, o módulo da força exercida pelo bloco A sobre o bloco B é: (g=10m/s²)

a) 26,4N                    b) 28,5N                    c) 32,4N                    d) 39,2N                      e) 48,4N

06-(UNESP-SP) Dois blocos idênticos, A e B, se deslocam sobre uma mesa plana sob ação de uma força de 10N, aplicada em A, conforme ilustrado na figura.

Se o movimento é uniformemente acelerado, e considerando que o coeficiente de atrito cinético entre os blocos e a mesa é m = 0,5, a força que A exerce sobre B é:

a) 20N.                    b) 15N.                    c) 10N.                      d) 5N.                      e) 2,5N.

07-(UNESP-SP) A figura ilustra um bloco A, de massa m_A = 2,0 kg, atado a um bloco B, de massa m_B = 1,0 kg, por um fio inextensível de massa desprezível. O coeficiente de atrito cinético entre cada bloco e a mesa é m. Uma força F = 18,0 N é aplicada ao bloco B, fazendo com que ambos se desloquem com velocidade constante.

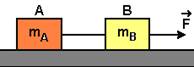
Considerando g = 10,0 m/s², calcule

a) o coeficiente de atrito m.

b) a tração T no fio.

08-(UFV-MG) Três blocos idênticos, A, B e C, cada um de massa M, deslocam-se sobre uma superfície plana com uma velocidade de módulo V constante. Os blocos estão interligados pelas cordas 1 e 2 e são arrastados por um homem, conforme esquematizado na figura a seguir.

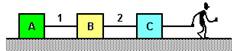
O coeficiente de atrito cinético entre os blocos e a superfície é m e a aceleração da gravidade local é g. Calcule o que se pede em termos dos parâmetros fornecidos:

a) a aceleração do bloco B.

b) a força de tensão T na corda 2.

09-(UNESP-SP) Um caixote de massa 20kg está em repouso sobre a carroceria de um caminhão que percorre uma estrada plana, horizontal, com velocidade constante de 72km/h. Os coeficientes de atrito estático e dinâmico entre o caixote e o piso da carroceria, são aproximadamente iguais e valem m=0,25 (admitir g=10m/s²)

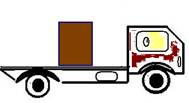
a) Qual é a intensidade da força de atrito que está agindo sobre o caixote? Justifique.

b) Determine o menor tempo possível para que esse caminhão possa frear sem que o caixote escorregue.

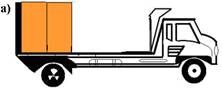
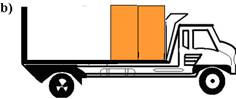
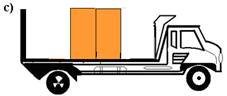
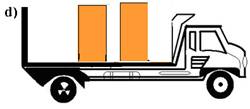
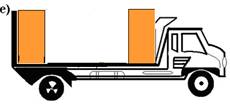
10- (UFJF-MG) Um caminhão é carregado com duas caixas  de madeira, de massas iguais a 500kg, conforme mostra a figura.

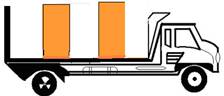
O caminhão é então posto em movimento numa estrada reta e plana, acelerando até adquirir uma velocidade de 108km/h e depois é freado até parar, conforme mostra o gráfico. (g=10m/s²).

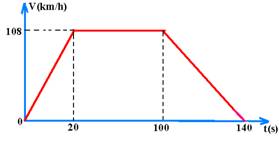
O coeficiente de atrito estático entre as caixas e a carroceria do caminhão é m=0,1. Qual das figuras abaixo melhor representa a disposição das caixas sobre a carroceria no final do movimento?

      

   

11- (UFRJ-RJ) Uma força horizontal de módulo F puxa um bloco sobre uma mesa horizontal com uma aceleração de módulo a, como indica a figura 1

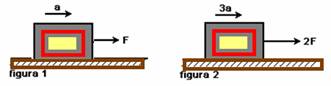
Sabe-se que, se o módulo da força for duplicado, a aceleração terá módulo 3a, como indica a figura 2. Suponha que, em ambos os casos, a única outra força horizontal que age sobre o bloco seja a força de atrito - de módulo invariável f - que a mesa exerce sobre ele.

Calcule a razão f/F entre o módulo f da força de atrito e o módulo F da força horizontal que puxa o bloco.

12- (Ufrrj-RJ) Dois carros de corrida são projetados de forma a aumentar o atrito entre os pneus e a pista. Os projetos são idênticos, exceto que num deles os pneus são mais largos e no outro há um aerofólio. Nessas condições podemos dizer que

a) em ambos os projetos, o atrito será aumentado em relação ao projeto original.

b) em ambos os projetos, o atrito será diminuído em relação ao projeto original.

c) o atrito será maior no carro com aerofólio.

d) o atrito será maior no carro com pneus mais largos.

e) nenhum dos projetos alterará o atrito.

13-(UNESP-SP) Dois blocos, A e B, com A colocado sobre B, estão em movimento sob ação de uma força horizontal de 4,5 N aplicada sobre A, como ilustrado na figura.

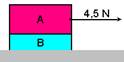
Considere que não há atrito entre o bloco B e o solo e que as massas são respectivamente m_A = 1,8 kg e m_B = 1,2 kg. Tomando g = 10 m/s², calcule

a) a aceleração dos blocos, se eles se locomovem juntos.

b) o valor mínimo do coeficiente de atrito estático para que o bloco A não deslize sobre B.

14-(UNESP-SP) Um bloco de massa 2,0 kg repousa sobre outro de massa 3,0 kg, que pode deslizar sem atrito sobre uma superfície plana e horizontal. Quando uma força de intensidade 2,0 N, agindo na direção horizontal, é aplicada ao bloco inferior, como mostra a figura, o conjunto passa a se movimentar sem que o bloco superior escorregue sobre o inferior.

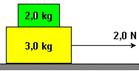
Nessas condições, determine (g=10m/s2)

a) a aceleração do conjunto.

b) a intensidade da força de atrito entre os dois blocos.

15-(PUC-RJ) Um certo bloco exige uma força F₁ para ser posto em movimento, vencendo a força de atrito estático. Corta-se o bloco ao meio, colocando uma metade sobre a outra.

Seja agora F₂ a força necessária para pôr o conjunto em movimento. Sobre a relação F₂ / F₁, pode-se afirmar que:

a) ela é igual a 2.          b) ela é igual a 1.          c) ela é igual a 1/2.          d) ela é igual a 3/2.

e) seu valor depende da superfície.

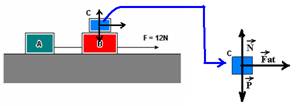
16-(UNESP-SP) Dois corpos, A e B, atados por um cabo, com massas m_A = 1 kg e m_B = 2,5 kg, respectivamente, deslizam sem atrito no solo horizontal sob ação de uma força, também horizontal, de 12 N aplicada em B. Sobre este corpo, há um terceiro corpo, C, com massa m_C = 0,5 kg, que se desloca com B, sem deslizar sobre ele. A figura ilustra a situação descrita

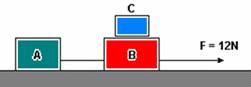
Calcule a força exercida sobre o corpo C.(g=10m/s²)

17-(UNIFESP-SP) A figura representa uma demonstração simples que costuma ser usada  para ilustrar a Primeira Lei de Newton.

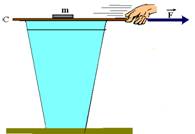
O copo, sobre uma mesa, está com a boca tampada pelo cartão C e, sobre este está a moeda m. A massa da moeda é 0,010kg e o coeficiente de atrito estático entre a moeda e o cartão é 0,15. O experimentador puxa o cartão com a força 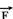, horizontal, e a moeda escorrega do cartão e cai dentro do copo.

a) Represente todas as forças que atuam sobre a moeda m  quando ela está escorregando sobre o cartão puxado pela força 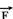. Nomeie cada uma das forças representadas.

b) Costuma-se explicar o que ocorre com a afirmação de que, devido à inércia, a moeda escorrega e cai dentro do copo. Isso é sempre verdade ou é necessário que o módulo de 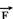 tenha uma intensidade mínima para que a moeda escorregue sobre o cartão? Se for necessária essa força mínima, qual é, nesse caso, o seu valor? (Despreze a massa do cartão, o atrito entre o cartão e o copo e admita g=10m/s²).

18-(UFAL)  A figura ilustra um pequeno bloco A, de massa 1 kg, sobre um grande bloco B, de massa 4 kg.

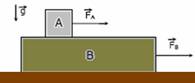
Não há atrito entre os blocos. As forças horizontais paralelas possuem módulos constantes F_A = 24 N e F_B = 12 N. Considerando a aceleração da gravidade g = 10 m/s² e o coeficiente de atrito cinético entre o bloco B e a superfície horizontal igual a 0,2,  determine o módulo da aceleração relativa entre os blocos, enquanto um bloco estiver sobre o outro.

19-(PUC-MG) Um bloco de massa 3,0 kg é pressionado contra uma parede vertical por uma força de intensidade F conforme ilustração.

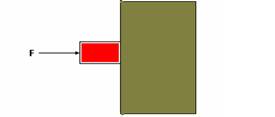
 Considere a gravidade como 10m/s², o coeficiente de atrito estático entre o bloco e a parede como 0,20 e o coeficiente de atrito cinético como 0,15.

O valor máximo da força F para que o bloco desça em equilíbrio dinâmico é de:

a) 125 N                    b) 200 N                    c) 250 N                     d) 150 N                    e) 500 N

20--(UFAL) O bloco da figura possui peso P e se encontra na iminência de movimento sob a ação de uma força de módulo constante F e direção perpendicular à parede vertical. Se o coeficiente de atrito estático entre a parede e o bloco é menor que

1, assinale a relação correta entre P e F.

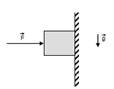
A) 0 < P < F            B) F < P < 2F            C) 0 < F < P/2            D) P/2 < F < P            E) 0 < F < P

21- (UERJ-RJ) Uma pessoa de massa igual a 80 kg encontra-se em repouso, em pé sobre o solo, pressionando perpendicularmente

uma parede com uma força de magnitude igual a 120 N, como mostra a ilustração a seguir.

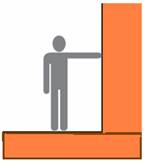
A melhor representação gráfica para as distintas forças externas que atuam sobre a pessoa está indicada em:

22-(UERJ-RJ) Com relação ao exercício anterior, considerando a aceleração da gravidade igual a 10 m . s ^-2, o coeficiente de atrito entre a superfície do solo e a sola do calçado da pessoa é da ordem de:

(A) 0,15                    (B) 0,36                    (C) 0,67                    (D) 1,28

23-(UNIFESP-SP) A figura representa um bloco B de massa m_B apoiado sobre um plano horizontal e um bloco A de massa m_A a ele pendurado. O conjunto não se movimenta por causa do atrito entre o bloco B e o plano, cujo coeficiente de atrito estático é m_B.

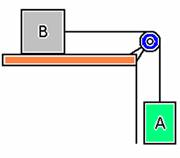
Não leve em conta a massa do fio, considerado inextensível, nem o atrito no eixo da roldana. Sendo g o módulo da aceleração da gravidade local, pode-se afirmar que o módulo da força de atrito estático entre o bloco B e o plano

a) é igual ao módulo do peso do bloco A.

b) não tem relação alguma com o módulo do peso do bloco A.

c) é igual ao produto m_B . g . m_B, mesmo que esse valor seja maior que o módulo do peso de A.

d) é igual ao produto m_B . g . m_B, desde que esse valor seja menor que o módulo do peso de A.

e) é igual ao módulo do peso do bloco B.

24-(Unisanta-SP) No sistema representado a seguir, os corpos A, B e C tem massas respectivamente iguais a 3kg, 2kg e 7kg.

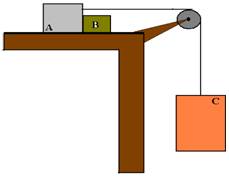
Os blocos A e C são ligados por um fio leve e flexível. A polia é ideal e o coeficiente de atrito dos blocos A e B com a superfície é igual a m=0,2. A aceleração dos blocos e a força de contato entre os blocos A e B valem, respectivamente (g=10m/s²):

a) 5m/s² e 35N      b) 5m/s² e 14N      c) 6m/s² e 14N      d) 8m/s² e 35N      e) 6m/s²  e 35N.

25-(PUC-MG) Determine massa mínima que deve ser colocada sobre o bloco de 10 kg para mantê-lo em equilíbrio, sabendo-se

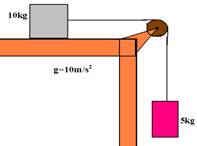
que o coeficiente de atrito estático entre ele e a mesa é 0,20. (g=10m/s^2.).

26-(UnB-DF) O coeficiente de atrito estático entre os blocos A e B, montados como mostra a figura abaixo, é de 0,9.

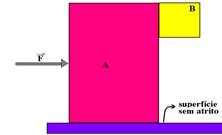
Considerando que as massas dos blocos A e B sejam, respectivamente, iguais a 5,0kg e 0,4kg e que g=10m/s², calcule em newtons, o menor valor do módulo da força  para que o bloco B não caia.

27-(UNIFESP-SP) A figura representa um caixote transportado por uma esteira horizontal. Ambos tem velocidade de módulo V, constante,, suficientemente pequeno para que a resistência do ar sobre o caixote possa ser considerada desprezível.

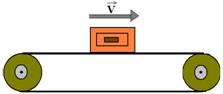
Pode-se afirmar que sobre esse caixote, na situação da figura.

a) atuam quatro forças: o seu peso, a reação normal da esteira, a força de atrito entre a esteira e o caixote e a força motora que a esteira exerce sobre o caixote.

b) ) atuam três forças: o seu peso, a reação normal da esteira, a força de atrito entre a esteira e o caixote, no sentido oposto ao do movimento.

c) ) atuam três forças: o seu peso, a reação normal da esteira, a força de atrito entre a esteira e o caixote, no sentido do movimento..

d) ) atuam duas forças: o seu peso, a reação normal da esteira.

e) não atua força nenhuma, pois ele tem movimento retilíneo uniforme.

28-(UFRJ-RJ) Considere um caminhão de frutas trafegando em movimento retilíneo numa estrada horizontal, com velocidade uniforme de V=20m/s. O caminhão transporta, na caçamba, uma caixa de maçãs de massa m=30kg.

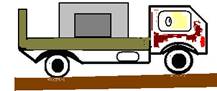
 Ao avistar um sinal de trânsito a 100m, o motorista começa a frear uniformemente, de modo a parar junto a ele.

a) Faça um esquema das forças que atuam sobre a caixa durante a frenagem.

b) Calcule o módulo da componente horizontal da força que o chão da caçamba do caminhão exerce sobre a caixa durante a frenagem.

29-(UFPE) Uma caixa de massa 10kg é ligada a um bloco de massa 5kg, por meio de um fio fino e inextensível que passa por uma pequena polia sem atrito, como mostra a figura.

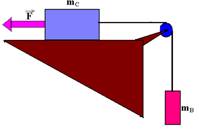
Determine o valor da força horizontal 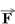, em N,  que deve ser aplicada a caixa de modo que o bloco suba, com aceleração a=2,0m/s². O coeficiente de atrito dinâmico entre a caixa e o piso é m=0,10. Considere g=10m/s².

30-(UFPE) Uma vassoura, de massa 0,4 kg, está posicionada sobre um piso horizontal como indicado na figura. Uma força, de módulo F(cabo), é aplicada para baixo ao longo do cabo da vassoura.

 Sabendo-se que o coeficiente de atrito estático entre o piso e a base da vassoura é m = 1/8, calcule F(cabo), em newtons, para que a vassoura fique na iminência de se deslocar. Considere desprezível a massa do cabo, quando comparada com a base da vassoura

31-(UERJ-RJ) Uma caixa está sendo puxada por um trabalhador, conforme mostra a Figura 1.  Para diminuir a força de atrito entre a caixa e o chão, aplica-se, no ponto X, uma força f. O segmento orientado que pode representar esta força está indicado na alternativa:

32-(UFSCAR-SP) Um menino deseja deslocar um bloco de madeira sobre o chão horizontal puxando uma corda amarrada ao bloco.

 Sabendo-se que o coeficiente de atrito estático entre a madeira e o chão vale 0,4, que a massa do bloco é 42 kg e que a aceleração da gravidade é igual a 10 m/s², e considerando Ö3 = 1,7, qual a menor intensidade da força que o menino deve puxar a corda para deslocar o bloco, se a direção da corda forma com o chão um ângulo de 60°?

a) 100 N.                    b) 200 N.                    c) 220 N.                    d) 250 N.                    e) 300 N.

33-(UNESP-SP) Na figura está representada esquematicamente a força 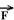 arrastando o bloco de massa 2,0kg com aceleração constante de 0,1m/s² sobre o plano horizontal.

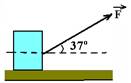
(Dados: cos37^o=0,8; sen37^o=0,6 e g=10m/s²). Sendo F_at=0,6N a força de atrito entre o bloco e o plano, pode-se afirmar que o módulo de 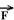, em N, é:

a) 0,5                     b) 1,0                      c) 1,5                      d) 2,0                       e) 2,5

34-(UFES) Dois corpos de massas m_A e m_B (m_B>m_A) estão ligados por um fio inextensível e de massa desprezível conforme a figura abaixo.

Dois mancais exercem, cada um, uma força horizontal de intensidade N sobre o corpo A. O coeficiente de atrito dinâmico entre os mancais é m, e a aceleração da gravidade  g é conhecida. Considere que o fio desliza livremente sobre as duas polias e que estas possuem massas desprezíveis. Estando os corpos em movimento, determine:

a) a aceleração com que os corpos A e B se deslocam.

b) a intensidade da força N que cada um dos mancais deve exercer sobre o corpo A, para que os corpos A e B se desloquem com velocidade constante.

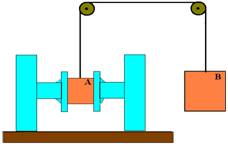
35-(UNICAMP-SP) Considere, na figura ao lado, dois blocos A e B, de massas conhecidas, ambos em repouso.

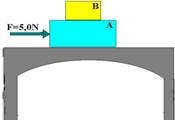
Uma força de 5,0N é aplicada no bloco A, que permanece em repouso. Há atrito entre o bloco A e a mesa, e entre os blocos A e B.

a) O que acontece com o bloco B?

b) Reproduza a figura, indicando as forças horizontais(sentido, módulo e onde estão aplicadas) que atuam sobre os blocos A e B.

36-(UFBA) Um corpo A pesa 100N e está em repouso sobre o corpo B, que pesa 200N. O corpo A está ligado por uma corda ao anteparo C, enquanto o corpo B está sendo solicitado por uma força horizontal F, de 125N. O coeficiente de atrito de escorregamento entre os corpos A e B é 0,25.

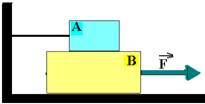
Determine o coeficiente de atrito entre o corpo B e a superfície de apoio e a tração na corda, considerando o corpo B em movimento iminente.

37-(ITA-SP) Os blocos A e B da figura tem massa m. O coeficiente de atrito entre todas as superfícies é m. A força 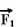 imprime ao bloco B da figura (I) velocidade uniforme.

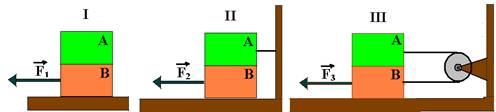
Calcule as relações F₂/F₁ e F₃/F₁, nas quais F₂ é a força indicada na figura (II) e F₃ é indicada na figura (III). Para que o bloco B nessas figuras tenha velocidade constante.

38-(UFF-RJ) Um pano de prato retangular, com 60cm de comprimento e constituição homogênea, está em repouso sobre uma mesa, parte sobre sua superfície, horizontal e fina, e parte pendente, como mostra a figura.

Sabendo-se que o coeficiente de atrito estático entre a superfície da mesa  e o pano é igual a 0,5 e que o pano está na iminência de deslizar, pode-se afirmar que o comprimento L da parte sobre a mesa é:

a) 40cm                    b) 20cm                     c) 15cm                       d) 60cm                     e) 30cm

39-(FUVEST-SP) O sistema indicado na figura a seguir, onde as polias são ideais, permanece em repouso graças à força de atrito entre o corpo de 10kg e a superfície de apoio.

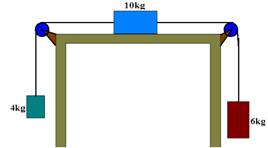
Determine o valor da força de atrito.

40-(UNESP-SP) Um trator  se desloca em uma estrada, da esquerda para a direita, com movimento acelerado. O sentido das forças de atrito que a estrada faz sobre as rodas do carro é indicado na figura a seguir:

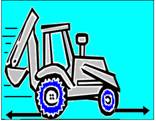
   É correto afirmar que:

  a) o trator tem tração nas quatro rodas;       b) o trator tem tração traseira;      c) o trator tem tração dianteira

  d) o trator está com o motor desligado;       e) a situação apresentada é impossível de acontecer.

41-(UERJ-RJ) Considere um carro de tração dianteira que acelera no sentido indicado na figura em destaque. O motor é capaz de impor às rodas de tração um determinado sentido de rotação. Só há movimento quando há atrito estático, pois, na sua ausência, as rodas de tração patinam sobre o solo, como acontece em um terreno enlameado. O diagrama que representa corretamente as forças de atrito estático que o solo exerce sobre as rodas é:

42-(ITA-SP) Um automóvel desloca-se sobre uma estrada, da esquerda para a direita, conforme as figuras de a a d. As setas nas rodas indicam os sentidos das forças de atrito (sem relação com os módulos) exercidas sobre elas pelo chão.

     

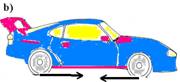
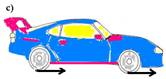
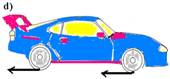
Associe as alternativas apresentadas com os algarismos romanos de I a IV.

I – Tração somente nas rodas dianteiras         II – Tração nas quatro rodas           III – Motor desligado (desacoplado)

IV – Tração somente nas rodas traseiras

43-(UNICAMP) Um caminhão transporta um bloco de ferro de 3,0t, trafegando horizontalmente e em linha reta, com velocidade constante. O motorista vê o sinal (semáforo) ficar vermelho e aciona os freios, aplicando uma desaceleração constante de valor 3,0 m/s². O bloco não escorrega.

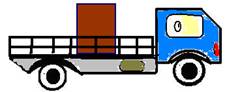
 O coeficiente de atrito estático entre o bloco e a carroceria é 0,40. Adote g = 10 m/s².

 a) Qual a intensidade da força de atrito que a carroceria aplica sobre o bloco, durante a desaceleração?

 b) Qual é a máxima desaceleração que o caminhão pode ter para o bloco não escorregar?

44- (UNIFESP-SP) Uma bonequinha está presa por um ímã a ela colado, à porta vertical de uma geladeira.

a) Desenhe esquematicamente essa bonequinha no caderno de respostas, representando e nomeando as forças que atuam sobre ela.

b) Sendo m = 20g a massa total da bonequinha com o ímã e μ = 0,50 o coeficiente de atrito estático entre o ímã e a porta da geladeira, qual deve ser o menor valor da força magnética entre o ímã e a geladeira para que a bonequinha não caia? Dado: g = 10 m/s².

45-(UFRJ-RJ) Uma força horizontal e de intensidade 30 N é aplicada num corpo A de massa 4,0 kg, preso a um corpo B de massa 2,0 kg que, por sua vez, se prende a um corpo C.

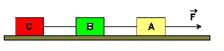
O coeficiente de atrito entre cada corpo e a superfície horizontal de apoio é 0,10 e verifica-se que a aceleração do sistema é, nessas condições, 2,0 m/s2. Adote g = 10 m/s² e analise as afirmações.

1) A massa do corpo é de 5,0kg    2) A tração no fio que une A a B tem módulo 18N

3) A força de atrito sofrida pelo corpo A vale 4,0N    4) a tração no fio que une B a C tem intensidade 8,0N

5) A força resultante no corpo B tem módulo 4,0N

46-(UNICAMP-SP) Ao se usar um saca-rolha, a força mínima que deve ser aplicada para que a rolha de uma garrafa comece a sair é igual a 360N.

 Sendo μ_e = 0,2 o coeficiente de atrito estático entre a rolha e o bocal da garrafa, encontre a força normal que a rolha exerce no bocal da garrafa. Despreze o peso da rolha.

47-(UFPE) Os blocos A, B e C da figura possuem a mesma massa m = 7,0 kg. O coeficiente de atrito cinético entre todas as superfícies é 0,3. Calcule o módulo da força F, em N, que imprime uma velocidade constante ao bloco B, levando-o desde a

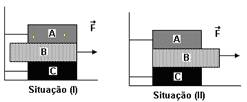
situação (1) até a situação (2). (g=10m/s²).

48-(FUVEST-SP) Procedimento de segurança, em auto estradas, recomenda que o motorista mantenha uma “distância” de dois segundos do carro que está à sua frente, para que, se necessário, tenha espaço para frear (“regra dos dois segundos”). Por essa regra, a distância D que o carro percorre, em dois segundos, com velocidade constante V_o, deve ser igual à distância necessária para que o carro pare completamente após frear. Tal procedimento, porém, depende da velocidade V_o com que o carro trafega e da desaceleração máxima a, fornecida pelos freios.

a) Determine o intervalo de tempo T_o, em segundos, necessário para que o carro pare completamente , percorrendo a distância D referida.

b) Represente, no sistema de eixos abaixo, a variação da desaceleração a, em função da velocidade V_o, para situações em que o carro pára completamente em um intervalo T_o(determinado no item anterior).

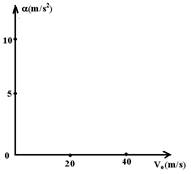
c) Considerando que a desaceleração a depende principalmente do coeficiente de atrito m entre os pneus e o asfalto, sendo 0,6 o valor de m, determine, a partir do gráfico, o valor máximo de velocidade V_M, em m/s, para o qual a regra dos dois segundos permanece válida.

49-(MACKENZIE-SP-09) Um bloco A, de massa 6 kg, está preso a outro B, de massa 4 kg, por meio de uma mola ideal de constante elástica 800 N/m. Os blocos estão apoiados sobre uma superfície horizontal e se movimentam devido à ação da força 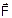 horizontal, de intensidade 60 N. Sendo o coeficiente de atrito cinético entre as superfícies em contato igual a 0,4, a distensão da

mola é de: Dado: g = 10m/s²

a) 3 cm                                b) 4 cm                                  c) 5 cm                                  d) 6 cm                                       e) 7 cm

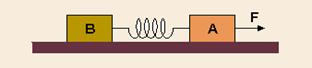
50-(MACKENZIE-SP-010) Um corpo de peso 30 N repousa sobre uma superfície horizontal de coeficiente de atrito estático 0,4. Por meio de uma mola de massa desprezível, de comprimento natural 20 cm e constante elástica 20N/m, prende-se esse corpo em uma parede como mostra a figura. A máxima distância a que podemos manter esse corpo da parede e em equilíbrio será de

a) 26 cm                       b) 40 cm                               c) 80 cm                                d) 90 cm                               e) 100 cm 

51-(CPS-010)  Para evitar que seus pais, que já são idosos, não sofram acidentes no piso escorregadio do quintal da casa,  Sandra

 contratou uma pessoa para fazer ranhuras na superfície desse piso – atitude ecoprática que não gera entulho, pois torna

desnecessária a troca do piso. O fato de o piso com ranhuras evitar que pessoas escorreguem está ligado ao conceito físico de

a) atrito.                         b) empuxo.                       c) pressão.                        d) viscosidade.                       e) condutibilidade. 

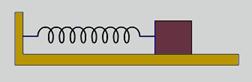
52-(CFT-MG-010)  Em uma superfície horizontal, uma caixa é arrastada para a direita, sob a ação de uma força constante F e de uma força de atrito F_at conforme a figura.

Considerando essa situação, a alternativa correta é

Se a caixa está em movimento retilíneo, temos as seguintes hipóteses:

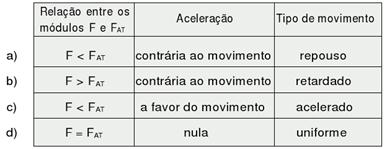
53-(UFG-GO)  A força muscular origina-se nas fibras musculares, conforme figura (a), como resultado das interações entre certas proteínas que experimentam mudanças de configuração e proporcionam a contração rápida e voluntária do músculo.

A força máxima que um músculo pode exercer depende da sua área da seção reta e vale cerca de 30 N/cm². Considere um operário que movimenta com uma velocidade constante uma caixa de 120 kg sobre uma superfície rugosa, de coeficiente de atrito 0,8, usando os dois braços, conforme ilustrado na figura (b).

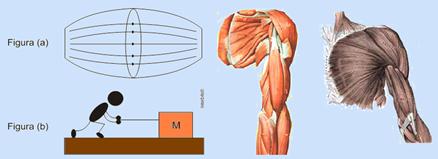
Dessa forma, a menor seção reta dos músculos de um dos braços do operário, em cm2, e uma das proteínas responsáveis pela contração das miofibrilas são:

Dados: g =10,0 m/s²

a) 16 e actina.                      b) 16 e mielina.                       c) 20 e miosina.                     d) 32 e actina.                    e) 32 e miosina.  

54- (UFLA-AL-010)  Um trator utiliza uma força motriz de 2000 N e arrasta, com velocidade constante, um tronco de massa 200

Kg ao longo de um terreno horizontal e irregular. Considerando g = 10 m/s2, é correto afirmar que o coeficiente de atrito cinético μ_c entre o tronco e o terreno é:

a) 1,0                                            b) 0,5                                               c) 0,25                                                d) zero  

55-(UNESP-SP-011)  As figuras 1 e 2 representam dois esquemas experimentais utilizados para a determinação do coeficiente de atrito estático entre um bloco B e uma tábua plana, horizontal.

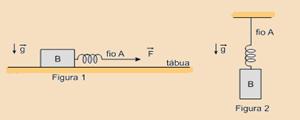
No esquema da figura 1, um aluno exerceu uma força horizontal 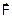 no fio A e mediu o valor 2,0 cm para a deformação da mola, quando a força  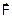atingiu seu máximo valor possível, imediatamente antes que o bloco B se movesse. Para determinar a massa do bloco B, este foi suspenso verticalmente, com o fio A fixo no teto, conforme indicado na figura 2, e o aluno mediu a deformação da mola igual a 10,0 cm, quando o sistema estava em equilíbrio. Nas condições descritas, desprezando a resistência do ar, o coeficiente de atrito entre o bloco e a tábua vale

a) 0,1.                                b) 0,2.                                        c) 0,3.                                      d) 0,4.                                           e) 0,5.  

56-(UNICAMP-SP-011)Acidentes de trânsito causam milhares de mortes todos os anos nas estradas do país. Pneus desgastados (“carecas”), freios em péssimas condições e excesso de velocidade são fatores que contribuem para elevar o número de acidentes de trânsito.

O sistema de freios ABS (do alemão “Antiblockier-Bremssystem”) impede o travamento das rodas do veículo, de forma que elas

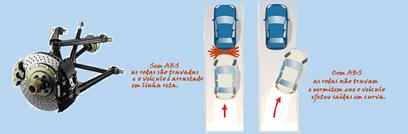
não deslizem no chão, o que leva a um menor desgaste do pneu. Não havendo deslizamento, a distância percorrida pelo veículo até a parada completa é reduzida, pois a força de atrito aplicada pelo chão nas rodas é estática, e seu valor máximo é sempre maior que a força de atrito cinético. O coeficiente de atrito estático entre os pneus e a pista é μ_e= 0,80 e o cinético vale μ_c = 0,60. Sendo g = 10 m/s² e a massa do carro m = 1200 kg, o módulo da força de atrito estático máxima e a da força de atrito cinético são, respectivamente, iguais a

a) 1200 N e 12000 N.                    b) 12000 N e 120 N.                      c) 20000 N e 15000 N.               d) 9600 N e 7200 N.  

57-(UFAL-AL-011) Uma criança tenta puxar a sua caixa de brinquedos, de peso P, exercendo uma força de tensão numa corda ideal, de módulo F e direção perfazendo um ângulo θ com a horizontal (ver figura)

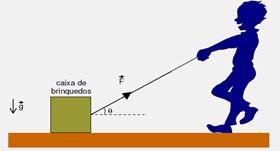
O coeficiente de atrito estático entre a caixa e o solo horizontal é denotado por μ_e. Assinale a expressão para o máximo valor de

F de modo que a caixa ainda permaneça em repouso. (Para efeito de cálculo, considere a caixa como uma partícula material.)

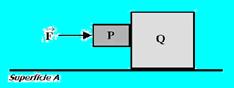
58-(UPE-PE-011) Sejam os blocos P e Q de massas m e M, respectivamente, ilustrados na figura a seguir. O coeficiente de

atrito estático entre os blocos é μ, entretanto não existe atrito entre o bloco Q e a superfície A. Considere g

a aceleração da gravidade.

A expressão que representa o menor valor do módulo da força horizontal F para que o bloco P não caia, é

     

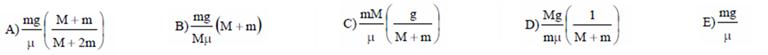
59-(UFPR-PR-011) Um esporte muito popular em paises do Hemisfério Norte é o “curling”, em que pedras de granito polido são

lançadas sobre uma pista horizontal de gelo. Esse esporte lembra o nosso popular jogo de bocha. Considere que um jogador tenha arremessado uma dessas pedras de modo que ela percorreu 45 m em linha reta antes de parar, sem a intervenção de nenhum jogador. Considerando que a massa da pedra é igual a 20 kg e o coeficiente de atrito entre o gelo e o granito é de 0,02, assinale a alternativa que dá a estimativa correta para o tempo que a pedra leva para parar.

a) Menos de 18 s.          b) Entre 18 s e 19 s.           c) Entre 20 s e 22 s.          d) Entre 23 s e 30 s.          e) Mais de 30 s.

60-(UEM-PR-012)

Supondo que um bloco de massa m kg esteja sobre uma superfície plana e horizontal e que para mover esse bloco

uma força ligeiramente maior que  X N é necessária, assinale o que for correto.

01) A força de atrito estático máxima é igual a X N.

02) O coeficiente de atrito estático entre a superfície e o bloco é igual a X/(mg), em que  g é a aceleração da gravidade, dada em metros por segundo ao quadrado.

04) O coeficiente de atrito cinético entre a superfície e o bloco é maior que X/(mg), em que g é a aceleração da gravidade, dada em metros por segundo ao quadrado.

08) No S.I., tanto os coeficientes de atrito cinético e estático são dados em newtons.

16) A força de atrito estático é sempre maior que a força de atrito cinético.

61-(PUC-RS-012)

 Freios com sistema antibloqueio (ABS) são eficientes em frenagens bruscas porque evitam que as rodas sejam

bloqueadas e que os pneus deslizem no pavimento. Essa eficiência decorre do fato de que a força de atrito que o pavimento exerce sobre as rodas é máxima quando

A) os pneus estão deslizando, porque o atrito cinético é maior que o estático máximo.

B) os pneus estão na iminência de deslizar, porque o atrito estático máximo é maior que o cinético.

C) o carro está parado, porque o atrito estático é sempre máximo nessa situação.

D) a velocidade do carro é constante, porque o atrito cinético é constante.

E) a velocidade do carro começa a diminuir, porque nessa situação o atrito cinético está aumentando.

62--(UEPA-PA-012)

A faixa de pedestres é uma conquista do cidadão, a qual vem se consolidando na construção de novas avenidas nas grandes cidades

brasileiras. Um motorista trafegando em uma avenida a 54 km/h observa um pedestre atravessando a faixa e aciona os freios, aplicando uma desaceleração constante no veículo, o qual pára  depois  de  5 s. Sabendo-se que o motorista conseguiu respeitar a faixa, afirma-se que o coeficiente de atrito entre os pneus e a estrada vale: (Dado: g = 10 m/s²)

a) 0,3                            b) 0,5                              c) 0,7                             d) 0,9                              e) 1,1

63-(MACKENZIE-SP-012)

Um corpo de 5 kg está em movimento devido à ação da força 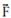, de intensidade 50 N, como mostra a figura.  

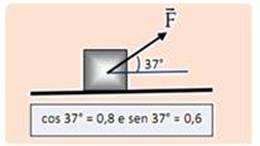
O coeficiente de atrito cinético entre a superfície de apoio horizontal e o bloco é 0,6 e a aceleração da gravidade no local tem módulo igual a 10 m/s^2.. A aceleração com a qual o corpo está se deslocando tem intensidade

a) 2,4 m/s²                   b) 3,6 m/s²                                 c) 4,2m/s²                             d) 5,6m/s²                             e) 6,2m/s²

64-(UENP-PR-012)

 Um bloco de massa M₁ = 10 kg, inicialmente em repouso em um plano horizontal, está ligado por um cabo ao bloco M₂ = 5 kg. Admitindo

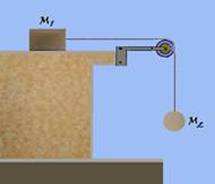
que o sistema esteja em equilíbrio estático, assinale o valor do coeficiente de atrito entre a superfície e o bloco. (g = 10 m/s²)

a) 0,18                              b) 0,27                           c) 0,50                             d) 0,60                                  e) 0,754

65--(UFF-RJ-012)

Ímãs são frequentemente utilizados para prender pequenos objetos  em superfícies metálicas planas e verticais, como quadros de avisos e portas de geladeiras.

Considere que um ímã, colado a um grampo, esteja em contato com a porta de uma geladeira . Suponha que a força magnética que o ímã faz sobre a superfície da geladeira é perpendicular a ela e tem módulo F_M.

. O conjunto imã/grampo tem massa m_o

.O coeficiente de atrito estático entre a superfície da geladeira e a do ímã é  μ_e

.Uma massa M está pendurada no grampo por um fio de massa desprezível, como mostra a figura.

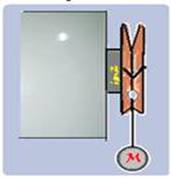
a) Desenhe no diagrama as forças que agem sobre o conjunto ímã/grampo (representado pelo ponto preto no

cruzamento dos eixos x e y na figura), identificando cada uma dessas forças.

b) Qual o maior valor da massa  M  que pode ser pendurada no grampo sem que o conjunto caia?

Resoluções

01- Calculando as intensidades das forças de atrito:

estático  ---  F_ate=m_e.N==m_e.P==m_e.mg=0,5.10.10  ---  F_atr=50N – ele só entra em movimento se F for superior a 50N  ---     dinâmico  ---  F_atd=m_d.N==m_e.P==m_d.mg=0,3.10.10  ---  F_atd=30N    

a) Se F=0, Fat=0, ele continua em repouso                 b) Se F=20N, F_ate=20N e ele continua em repouso    

c) Se F=40N, F_ate=40N e ele continua em repouso          d) Se F=50N, F_ate=50N e ele continua em repouso, mas está na iminência de movimento.          e) Se F=60N, ele entra em movimento e está acelerando com aceleração a tal que F_R=ma  ---  F – F_atd=ma  --- 

60 -   30=10a  ---  a=3/10  ---  a=3m/s² .

f) Como o bloco já está em movimento a força de atrito sobre ele é o dinâmico ou cinético e vale 30N.  ---  F_r=ma  ---

35 – 30=10.a  ---  a=5/10  ---  a=0,5m/s². Ele acelera com a velocidade aumentando de 0,5m/s em cada segundo.

g) Como F=30N e F_atd=30N, a força resultante sobre ele é nula e ele está em equilíbrio dinâmico, movendo-se em MRU.

h) Nesse caso a força resultante sobre ele é o F_atd=30N que o está freando com  ---  F_atd=ma  ---  30=10.a  ---  a=3m/s² e sua

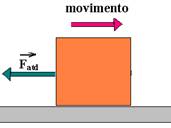
velocidade vai diminuindo de 3m/s em cada segundo, até parar.     

02- Pelo gráfico observamos que quando F=15N, a força de atrito estático é máxima e vale F_ate=15N. Qualquer força acima desse valor coloca o bloco em movimento. Quando F=30N, ele já entrou em movimento e o F_at sobre ele é o dinâmico e vale F_atd=10N (vide gráfico)  ---  F_R=ma  ---  30 – 10=5.a   ---  a=4m/s²    ---   F_ate=m_eN=m_eP=m_emg  ---  15=me.5.10  ---  m_e=15/50  ---  m_e=0,3

R- A

03- A única força que age sobre a caixa, na direção horizontal é a força de atrito dinâmico que é a força resultante, freando-o até parar.

V= V_o + a.t  ---  0 = 10 + a.5  ---  a= -2m/s² (negativo, pois está freando)  ---  em módulo a=2m/s²  ---  F_R=ma  ---  F_atd=ma  --- 

mN=ma  ---  mP =ma  ---  mmg=ma  ---  m=a/g  ---  m=2/10  ---  m=0,2  R- B

04- As forças verticais 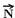 e 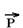se anulam, sobrando apenas a força de atrito dinâmico que é a força resultante sobre ele.

V_o=72km/h/3,6=20m/s  ---  Torricelli  ---  V² = V_o² + 2.a.DS  ---  0² = 20² + 2.a.50  ---  a=-400/100  --- a=-4m/s²  ---  em módulo  ---  a=4m/s²  ---  F_R=F_atd=m.a  ---  F_atd=10³.4  ---  F_atd=4.10³N  ---  V=V_o + a.t  ---  0=20 + (-4).t  ---  t=5s  ---  F_atd=m_dN=m_dP=m_dmg

4.10³=m_d.10³.10  ---  m_d=4.10³/10⁴  ---  m_d=0,4

05- Calculando a intensidade da força de atrito dinâmico que age sobre cada bloco

A  ---  F_atA=m_A.N_A  ---  F_atA=m_A.P_A  ---  F_atA=m_A.m_A.g  ---  F_atA=0,2.6.10  ---  F_atA=12N       

B  ---  F_atB=m_B.N_B  ---   F_atB=m_B.P_B  ---  F_atB=m_B.m_B.g  ---  F_atB=0,3.4.10  ---  F_atB=12N  

Colocando as forças na direção do movimernto que é horizontal:

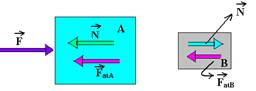
Bloco A  ---  F_RA=m_A.a  ---  F – (N + F_atA)=m_Aa  ---  60 – N – 12=6.a  ---  48 – N=6.a  I

Bloco B  ---  F_RB=m_B.a  ---  N – F_atB=m_B.a  ---  N – 12=4.a  II

Somando membro a membro I com II  ---  36=10.a  ---  a=3,6m/s²  ---  N – 12=4.a  ---  N=12 + 4.3,6  ---  N=26,4N  R- A

06- Colocando as forças

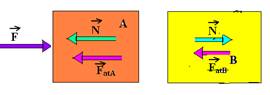
P_A=P_B=P

F_atA=m_A.N_A  ---  F_atA=m_A.P  ---  F_atA=0,5.P     

F_atB=m_B.N_B  ---   F_atB=m_B.P  ---  F_atB=0,5.P  

Bloco A ---  F_R=m.a  ---  F – (N + F_atA)=m.a  ---  10 – N – 0,5P=m.a I

Bloco B  ---  F_R=m.a  ---  N – F_atB=m.a  ---  N – 0,5P=m.a II  ---  somando I com II  ---  10 – P=2m.a  ---  a=(10 – P)/2m III

Substituindo III em II  ---  N – 0,5P = m(10 – P)/2m  ---  N=0,5P + 5 – 0,5P  ---  N=5N R-D

07- F_atA=m.m_A.g  ---  F_atA=m.2.10  ---  F_atA=20m   ---   F_atB=mm_Bg  ---  F_atB=m.1.10  ---  F_atB=10m

a) Colocando as forças:

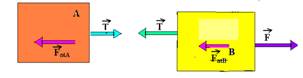
 Como os blocos estão com velocidade constante, estão em equilíbrio dinâmico e a força resultante sobre eles é nula  ---bloco B  ---  F_R=0 ---  F – F_atB – T=0  ---  18 - 10m - T=0  I   ---   bloco A  ---  F_R=0  ---  T - 20m=0  II  ---  somando I com II  ---  18 - 30m=0  --- m=0,6

b) T - 20m=0  ---  T=20.0,6  ---  T=12N

08- a) Fat_A=Fat_B=Fat_C=mMg   

 Como a velocidade é constante o sistema está em equilíbrio dinâmico e a força resultante sobre cada bloco é nula, assim, a=0.

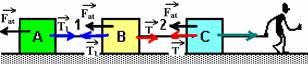
b) bloco B  --- F_r=0  ---  T=F_at + T₁  ---  T= mMg + T₁ I      ---   bloco A  ---  F_R=0  ---  T₁=Fat  ---  T₁=mMg  II   --- substituindo II em I  ---  T=mMg

09- a) Como o caminhão e o caixote estão com velocidade constante (equilíbrio dinâmico) a força resultante sobre o caixote é nula e, se F_R=0, F_at também será nula.

b) A força resultante que age sobre o caixote, na direção do movimento é a força de atrito F_at que ele troca com a carroceria.

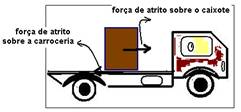
Sobre o caixote  ---  F_r=m.a  ---  F_at=m.a  ---  mmg=m.a  ---  0,25.10=a  ---  a=2,5m/s²   ---  a=2,5m/s²  ---  V=V_o + a.t  --- 

0 = 20 - 2,5.t  ---  t=20/2,5  ---  t=8s

10- A intensidade da força de atrito estático entre as caixa e a carroceria vale F_ate=mN  ---  F_ate=mP  ---  F_ate=mmg  ---  F_ate=0,1.500.10  ---  F_ate=500N (acima desse valor as caixas se movem).

No movimento acelerado  ---  V=V_o + a.t  ---  30=0 + a.20  ---  a=1,5m/s²   ---  F_R=m.a  ---  F_R=500.1,5  ---  F_R=750N ( como F_R>F_ate, as caixas se movem para trás e ficam juntas na parte traseira do caminhão).

No movimento uniforme, elas estão em equilíbrio dinâmico e F_R=0. Assim, elas não se movem e ficam juntas na parte traseira.

No movimento retardado  ---  V=V_o + a.t  ---  0=30 – a.40  ---  a=3/4m/s²  ---  F_R=m.a  ---  F_R=500.3/4  F_R=375N (menor que 500N, portanto elas não se movem e ficam na parte traseira do caminhão) R- A

11- A força de atrito sobre cada bloco é a mesma e vale f

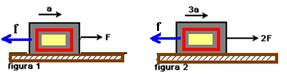
figura 1  ---  F_R=m.a  F – f=m.a I    ---    figura 2  ---  F_R=m.a  ---  2F – f=m.3.a II  ---  multiplicando I por (-1) e somando membro a membro I com II  ---  F=2ma III    ---    substituindo III em I  ---  f=ma IV    ---    dividindo membro a membro IV por III  --- 

f/F = 1/2

12- R- C (vide teoria)

13- a) Considerando os dois blocos como um corpo só de massa 3kg  ---  F_R=m.a  ---  4,5=3.a  ---  a=1,5m/s².

b) colocando as forças de atrito que os blocos A e B trocam entre si e que constituem par ação e reação (mesma intensidade,

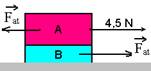
mesma direção e sentidos opostos) e aplicando F_R=m.a apenas no bloco B  ---  F_R=F_at=1,2.1,5  ---  F_at=1,8N  ---  agora, aplicando F_R=m.a apenas sobre o bloco A, teremos  ---  F_R=m.a  ---  4,5 – F_at=1,6.1,5  ---  F_at=1,8N  ---  F_at=mN  ---  F_at=mP  ---  F_at=mmg  --- 

1,8=m.1,8.10  ---  m=1,8/18  ---  m=0,1

14- a) F_R=(2,0 + 3,0).a  ---  2=5.a  ---  a=2/5  ---  a=0,4m/s².

b) colocando as forças de atrito que os blocos trocam entre si

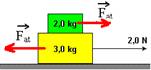
Bloco de baixo  ---  F_R=m.a  ---  2 – F_at=3.0,4  ---  F_at=0,8N

15- A força de atrito é a mesma nos dois casos:

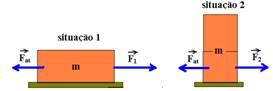
O F_at em cada situação é o mesmo, pois F_at=mP e m e P são os mesmos.

situação 1  ---  F_R=m.a  --- F₁ – F_at=ma  ---  F₁=F_at + ma I    ----    situação 2  ---  F_R=ma  ---  F₂ – F_at=ma II  ---  Observe em I e em II que F₁=F₂, portanto F₂/F₁=1 R- B

16- Cálculo da aceleração do sistema  ---   F_R=m.a  ---  12=(1 + 2,5 + 0,5).a  ---  a=3m/s² (aceleração dos três blocos).

Forças que atuam no corpo C:

Peso de C, aplicado pela Terra, de intensidade p=mg  ---  P=0,5.10com módulo 5,0 N.

Força normal para cima, aplicada por B sobre C, de intensidade N=5,0N (C está em equilíbrio vertical).

Força de atrito que B aplica sobre C  ---  F_R=m.a  ---  F_at=0,5.3  ---  F_at=1,5N

Observação: As forças 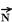 e 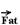podem ser somadas vetorialmente e se tornarem uma única força de B sobre C que chamamos de

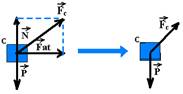
 força de contato 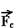 e que tem intensidade (F_C)²=(1,5)² + (5)²  ---  F_C=5,2N

17- a) Quando o cartão é puxado pela força 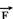, horizontal e para a direita, ele aplica sobre a moeda uma força de atrito cinético (dinâmico) 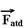, puxado-a também para a direita.

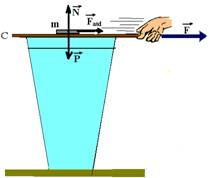
Sobre a moeda, além de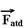 ´(horizontal e para a direita) agem também as força verticais:  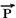(peso da moeda) e 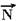(força normal exercida pelo cartão).

b) O Princípio da Inércia afirma que todo corpo em repouso, por inércia, tende a permanecer em repouso, mas somente se a força resultante sobre ele for nula e, no caso da moeda esse princípio não é válido, pois existe atrito ().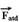

Vamos calcular a força de atrito estático  ---  F_ate=mN  ---  F_ate=mP  ---  F_ate=mmg  ---  F_ate=0,15.0,01.10  ---  F_ate=0,15N (para qualquer valor de F maior que 0,15N, a moeda entra em movimento, ou seja, destaca-se do cartão.

Assim, se F for maior que 0,15N a moeda poderá cair dentro do copo e se F for menor ou igual a 0,15N, a moeda acompanhará o cartão e não se destacará dele.

18- Como entre o bloco A e o bloco B não há atrito, a força resultante, na direção do movimento, sobre o bloco A será  ---  F_R=F_A=

M_A.a_A  ---  24=1.a_A  ---  a_A=24m/s²

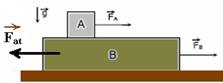
Entre o bloco B e o solo existe atrito que vale F_at=mN  ---  F_at=m(P_A + P_B)  ---  F_at=0,2.50  ---  F_at=10N  --- bloco B  ---  F_R=m_B.a_B  ---  F_B – F_at=4.a_B  ---  12 – 10=4.a_B  ---  a_B=0,5m/s²

Assim, a aceleração relativa entre A e B é de a=24 – 0,5  ---  a=23,5m/s².

19-Colocando todas as forças que agem sobre o bloco e sobre a parede

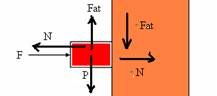
  equilíbrio na vertical  ---  F_at=P=mg=3.10  ---  F_at=30N  ---  equilíbrio na horizontal  ---  F=N  ---  F_at=mN  ---  30=0,2.F  --- 

F=30/0,2  ---  F=150N  R- D

20-No equilíbrio estático na iminência de movimento, a força de atrito estática é dada por μeN, e se equilibra com o peso P. Na situação do exercício, a força normal N é tal que N = F. Assim, μeN = P implica em μe = P/F. Se μe < 1, logo 0 < P < F. R- A

21- Colocando todas as forças que se relacionam com a pessoa, a parede e o solo.

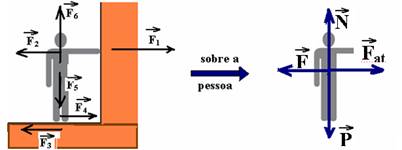
F₁ e F₂  ---  forças trocadas entre a pessoa e a parede de intensidade 120N  ---   F₃ e F₄  ---   forças de atrito trocadas entre os pés da pessoa e o solo  ---  F₅  ---  peso da pessoa trocada com o centro da Terra e F₆, força normal que a pessoa troca com o solo.

Como a pessoa está em repouso, a força resultante é nula e as forças verticais e horizontais se anulam  R- D

22- Calculando a intensidade da força de atrito  que age sobre a pessoa  ---  F_at=mN  ---  F_at=mP  ---  F_at=mmg  ---  F_at=m80.10  ---

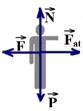
 F_at=800m  ---  mas, F_at=F=120N (equilíbrio horizontal)  ---  120=800m  ---  m=120/800  ---  m=0,15  R- A

23- Colocando as forças que agem sobre cada bloco na direção do movimento

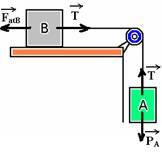
Observe que, como os blocos estão em equilíbrio  ---  P_A=T e T=F_atB. Assim, F_atB=P_A    R- A

24- Colocando as forças sobre cada bloco na direção do movimento

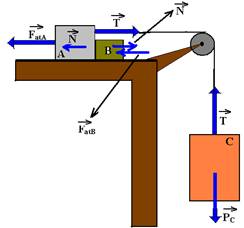
F_atA=mm_Ag  ---  F_atA=0,2.3.10  ---  F_atA=6N  ---  F_atB=mm_Bg  ---  F_atB=mm_Ag  ---  F_atB=0,2.2.10  ---  F_atA=4N  ---  P_C=m_C.g  ---

P_C=7.10  ---  P_C=70N

bloco C  ---  desce  ---  F_R=m_Ca  ---  P_C – T=m_C.a  ---  70 – T=7.a  I  ---  bloco B  ---  F_R=m_B.a  ---  N – 4=2.a  II  ---  bloco A   --- 

F_R=m_A.a  ---  T – N – 6=3.a  III   ---   somando membro a membro I, II e II  ---  70 – 10=12.a  ---  a=5m/s²

A força de contato entre A e B é N  ---  substituindo a=5m/s²  em II  ---  N – 4=2.5  ---  N=14N  R- B

25- Colocando o bloco de massa m sobre o bloco de massa 10kg e todas as forças que influem na tendência de movimento:

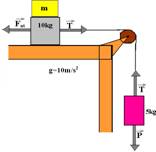
Como o sistema está em repouso, a força resultante sobre cada bloco é nula  ---  bloco de massa 5kg  ---  F_R=0  ---  P=T=5.10  --- 

T=50N  ---  blocos apoiados na superfície horizontal  ---  F_at=T  ---  mN=50  ---  m(P_10kg + P_m)=50  ---   0,2.(10 + m).10=50  --- 

20 + 2m=50  ---  m=30/2  ---  m=15kg    (para qualquer m³15kg colocada sobre 10kg, o sistema se moverá no sentido horário).

26- 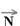  ---  força que o bloco A troca com o bloco B  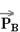---   - peso do bloco B  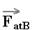---   - força de atrito que o bloco A aplica no bloco B, impedindo-o de escorregar.

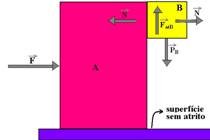
bloco B  ---  equilíbrio vertical  ---  F_atB=P=mg=0,4.10  ---F_atB=4N  ---  F_atB=mN  ---  4=0,9N  ---  N=4,4N

cálculo da aceleração de B em movimento horizontal para a direita onde a força resultante é 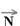 ---  F_R=m_B.a_B  ---   N=m_B.a_B  ---

4,4=0,4.a_B  ---  a_B=11m/s²  ---  mas, para o bloco B não cair e acompanhar o bloco A eles devem ter a mesma aceleração, ou seja,

a_A=11m/s²  ---  bloco A  ---  F_r=m_A.a_A  ---  F – N=m_A.a_A  ---  F – 4,4=5.11  ---  F=59,4N(para qualquer F³59,4N, o bloco B não cairá).

27- R –D Como o movimento é retilíneo uniforme, a força resultante sobre o caixote na direção do movimento (horizontal) é nula e , na vertical, a força peso e a reação normal da esteira se anulam. 

28- a) 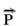- peso da caixa  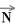---  - força normal que a caçamba aplica sobre a caixa  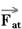---   - força de atrito trocada entre a caçamba e a caixa.

b) Essa força pedida é a força de atrito F_at  ---   Cálculo da aceleração do caminhão por Torricelli  ---  V²=V_o² + 2.a.DS  ---  0²=(20)² – 2.a.100  ---  a=2m/s²

Se a caixa não se mover em relação ao caminhão eles terão a mesma aceleração de 2m/s²e a força resultante  na direção horizontal vale  ---  F_R=m.a  ---  F_at=m.a  ---  F_at=30.2  ---  F_at=60N

29- Colocando as forças

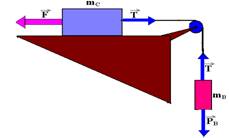
m_B  ---  sobe com a=2m/s²  ---  F_R=m_B.a  ---  T – 50=5.2  ---  T=60N  ---  bloco C se move para a esquerda com aceleração de 2m/s²  ---  F_R=m_C.a  ---F – T=m_C.a  ---  F – 60=10.2  ---  F=80N

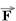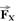30- Colocando as forças e decompondo em  e em  :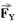

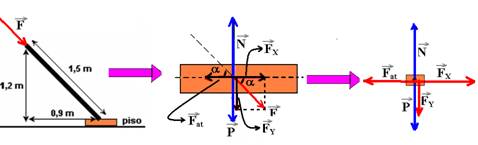
sena=1,2/1,5=0,8  ---   cosa=0,9/1,5=0,6  ---  F_X=Fcosa=F.0,6  ---  F_X=0,6F  ---  F_Y=Fsena=F.0,8  ---  F_Y=0,8F  ---  P=mg=0,4.10  ---  P=4N  ---  estando o sistema em equilíbrio estático, F_X=F_at e N=P + F_Y  ---  F_X=F_at  ---  0,6F=mN  ---

 0,6F=m(P + F_Y)  ---  0,6F=1/8.(4 + 0,8F)  ---  0,6F=4/8 + 0,8F/8  ---  0,6F=0,5 + 0,1F  ---  0,5F=0,5  ---  F=1N (para qualquer valor de F£1N, a vassoura não se deslocará).

31- Como F_at=mN, e como m é constante, das alternativas, a única força capaz de diminuir a força de com pressão N da caixa com o chão é a C

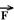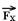32- Colocando as forças e decompondo em  e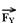 

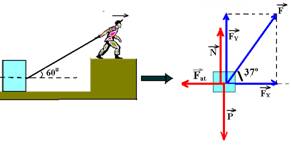
P=mg=42.10  ---  P=420N  ---  F_X=Fcos60^o=F.0,5  ---  F_X=0,5F  ---  F_Y=Fsen60^o=F.Ö3/2  ---  F_Y=0,85F

No equilíbrio estático temos, na horizontal F_at=F_X e na vertical, P=N + F_Y  ---  N=P - F_Y  ---  F_at=F_X  ---  mN=0,5F  ---  m(P - F_Y)=

0,5F  ---  0,4(420 - 0,85F)=0,5F  ---  168 - 0,34F=0,5F  ---  0,84F=168  ---  F=200N (qualquer valor acima de 200N desloca o bloco) R- C

33-Colocando as forças apenas na direção do movimento (horizontal):

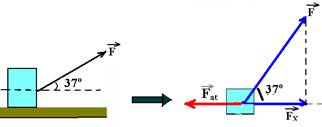
Como o movimento é na horizontal, vamos decompor  apenas em   ---  F_X=Fcos37^o  --- F_X=0,8F. 

Na horizontal  ---  F_R=ma  ---  F_X – F_at=ma  ---  0,8F – 0,6=2,0.0,1  ---  F=0,8/0,8  --- F=1,0N  R- B

34- a) como os corpos estão em movimento e como m_B>m_A, o sistema tem que se mover no sentido horário (A sobe e B desce). Colocando as forças:

- força horizontal que cada um dos mancais exerce sobre o corpo A  ---   - força de atrito que cada um dos mancais exerce sobre o corpo A tentando impedi-lo de subir e F_at=mN  ---  corpo A – sobe  ---  F_R=m_A.a  ---  T – P_{a­  –} 2F_at=m_A.a  ---  T – m_Ag - 2mN=m_A.a I  ---  corpo B – desce  ---  F_rm_B.a  --- P_B – T=m_B.a  ---  m_Bg – T=mB.a II  ---  somando membro a membro I com II  ---

m_Bg -  m_Ag - 2mN=m_A.a + m_B.a  --- ( m_B – m_A)g - 2mN=(m_A + m_B)a  ---  a=(m_B – m_A)g - 2mN /( m_A + m_B)

b) Se a velocidade é constante os corpos A e B estão em equilíbrio dinâmico e a força resultante sobre eles é nula.

corpo A  ---  F_R=0  ---  T = P_A + 2F_at  ---  T=m_Ag + 2mN I  ---  corpo B  ---  F_R=0  ---  T=P_B  ---  T=m_Bg II  ---  substituindo II em I  ---  m_Bg =m_Ag + 2mN  ---  N=(m_B - m_A)g /2m

35- a) continua em repouso

b) Sobre o bloco B não existe nenhuma força horizontal

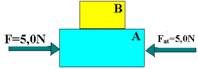
36- Colocando as forças sobre cada bloco

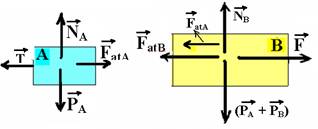
F_atA=m_A.N_A  ---  F_atA=m_A.P_A  ---  F_atA=0,25.100  ---  F_atA=25N   ---   como o sistema está repouso  ---  bloco A  ---   F_RA=0  ---  T=F_atA=25N   ---   bloco B  ---  F=F_atB + F_atA  ---  125=F_atB + 25  ---  F_atB=100N  ---  F_atB=m(P_A + P_B)  ---  100=m.300  ---  m=1/3

37- Como o coeficiente de atrito é o mesmo e o peso de cada bloco é também o mesmo a força de atrito entre A e B vale F_atA=mN  ---  F_atA=mP=F_at e entre B e o chão vale F_atB=mN=m(P_A + P_B)=m2P  ---  F_atB=2mP  ---  F_atB=2F_at.

Colocando todas as forças, em cada caso:

             

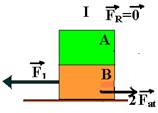
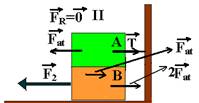
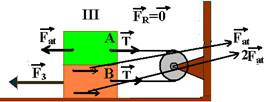
Situação I  ---  A- nenhuma força e B – F₁=2F_at  ---  situação II  ---  A – T=F_at e B –F₂=3F_at  ---  situação III  ---  A – T=F_at e

B – F₃=4F_at 

F₂/F₁=3F_at/2F_at  ---  F₂/F₁=1,5  ---  F₃/F₁=4F_at/2F_at  ---  F₃/F₁=2

38- Vamos chamar de L’, comprimento total do pano e de L’ – L o comprimento da parte pendente. Como o pano é de constituição homogênea, sua densidade é a mesma.

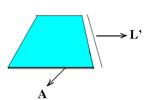
d=m_t/V_t  ---  d (densidade) – m_t (massa total) – V_t (volume total)  ---  m_t=d.V_t  ---  m_t=d.(A.L’), sendo A (área se seção transversal, espessura do pano) e L’ (comprimento total do pano)

massa apoiada – m_a=d.A.L e massa pendente – m_p=d.A.(L’ – L)

- peso da parte pendente  ---  P=m_pg (m_p, massa da parte pendente)  ---  a força de atrito entre o pano de comprimento L e a mesa está segurando o peso da parte pendente de comprimento (L’ – L), ou seja, F_at=P  ---  mm_ag= m_pg  ---  m.d.A.L.g=d.A.(L’ – L).g  ---   0,5.L=(60 – L)  ---  1,5L=60  ---  L=40cm R- A

39- Colocando as forças

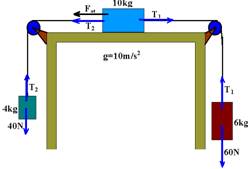
Observe na figura que a tendência de movimento é no sentido horário e, no bloco de massa 10kg a força de atrito estático é para a esquerda (contrário à tendência ao movimento).

Todos os blocos estão em repouso  ---  bloco de massa 4kg  ---  T₂=40N  ---  bloco de massa 6kg  ---  T₁=60N  ---bloco de massa 10kg  ---  T₁=T₂ + F_at  ---  60=40 + F_at  --- F_at=20N

40- Nas rodas com tração a força de atrito é a favor do movimento e nas rodas sem tração, contrária ao movimento. R- C

41- Nas rodas com tração a força de atrito é a favor do movimento e nas rodas sem tração, contrária ao movimento. R- B

42- I – A    II – C    III – D     IV – B   (vide resolução do exercício anterior)

43-  a) Fat=F_R=ma=3.10³.3  ---  F_at=9.10³N   b) Para o bloco não escorregar F_R=F_at  ---  ma=mmg  ---  a=mg=0,4.10  ---  a=4,0m/s²

44- a)Colocando as forças no imã-bonequinha:

 - força peso, vertical e para baixo aplicada pela Terra  ---  - força magnética aplicada pelo metal da parede da geladeira, atraindo o imã para ela  ---   - força normal de compressão trocada entre a geladeira e o imã  ---   - força de atrito entre a geladeira e o imã

b) equilíbrio vertical  ---  F_at=P  ---  mN=mg  ---  0,5.N=0,02.10  ---  N=0,2/0,5  ---  N=0,4N  ---  equilíbrio horizontal  ---  F_mag=N=0,4N

45- Cálculo da intensidade força de atrito F_at em cada bloco:

F_atA=mm_Ag=0,1.4.10  ---  F_atA=4,0N  ---  F_atB=mm_Bg=0,1.2.10  ---  F_atB=2,0N  ---  F_atC=mm_Cg=0,1m_C10  ---  F_atC=m_C ---  F_atA=4,0N  ---  F_atB=mm_Bg=0,1.2.10  --- F_atB=2,0N  ---  F_atC=mm_Cg=0,1m_C10  ---  F_atC=m_C

a=2,0m/s²

Colocando as forças na direção do movimento:

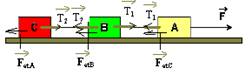
bloco A  ---   F_R=m_Aa  ---  30 – T₁ – 4=4.2  ---  T₁=18N  ---  bloco B  ---  F_R=m_Ba  ---  18 – 2 - T₂=2.2  ---  T₂=12N  ---  bloco C  --

F_R=m_Ca  ---  12= m_C.2  ---  m_C=6kg    ---  F_RB=18 – 14=4N

1 – F; 2 – V; 3 – V; 4 – F; 5 - V

46- F=F_at=mN  ---  360=0,2.N  ---  N=1,8.10³N

47- Sobre o bloco B, na direção do movimento agem as forças F_at1=mN  ---  F_at1=mP_A  ---  F_at1=mm_Ag  ---  F_at1=0,3.7.10  ---  F_at1=21N, que é a ação de A sobre B e F_at2=mN  ---  F_at2=m(P_A + P_B)  ---  F_at2=0,3.(70 + 70)  ---  F_at2=42N que é a reação de C sobre B.

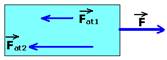
Como o bloco B se move com velocidade constante, F_RB=0  ---  F=F_at1 + F_at2  ---  F=21 + 42  ---  F=63N

48-

48-a) Distância D, percorrida com velocidade constante V_o

V=DS/Dt  ---  V_o=D/2

Distância D, percorrida com velocidade variando de V_o para 0, com desaceleração -a, no tempo t. 

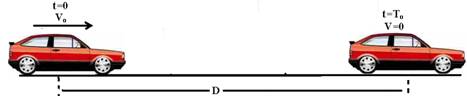
Torricelli  ---  V²=V_o² + 2.a.DS  ---  0²=V_o² + 2.(-a).D  ---  0²=(D/2)² – 2.a.D  ---  a=D/8 ---  V=V_o + a.t  ---  0=V_o + (-a).t

0=D/2 – (D/8).t  ---  t=4s

b) Relação entre a e V_o  ---  a=D/8  ---  V_o=D/2  ---  V_o=4a  ---  Trata-se de uma função do 1^o grau e o gráfico é uma reta, que é definida por apenas dois pontos, como por exemplo:

Quando a=0, V_o=0 (0,0) e quando a=10m/s², V_o=4.a  ---  V_o=4.10  ---  V_o=40m/s (40,10).

Colocando no gráfico:

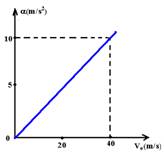
c) F_R=F_at  ---  ma=mmg  ---  a=0,6.10  ---  a=6m/s²  ---  quando a=6m/s², V_o=V_M e , pelo gráfico V_M»23,5m/s

49- No Bloco A na direção horizontal e sentido da força F é verdadeiro escrever  ---  F_R = m.a  ---  F – F(elástica) – F(atrito) = m.a  ---  F – k.x - m.m.g = m.a  ---  60 – 800.x – 0,4.6.10 = 6.a  ---  60 – 800.x – 24 = 6.a  ---  36 – 800.x = 6.a  ---  bloco B nas mesmas condições já citadas  ---  F_R = m.a  ---  F(elástica) – F(atrito) = m.a  ---  k.x - m.m.g = m.a  ---  800.x – 0,4.4.10 = 4.a  --- 

800.x – 16 = 4.a  ---  resolvendo, por adição, o sistema formado pelas duas equações  ---  36 – 800.x = 6.a  ---  800.x – 16 = 4.a  ---  36 – 16 = 10.a  ---  10.a = 20  ---  a = 20/10= 2 m/s²  ---  800.x – 16 = 4.a  ---   800.x = 16 + 4.2 = 16 + 8 = 24  ---   x =24/800  ---  x= 0,03 m = 3 cm  ---  R- A

50- A máxima distância (d) do bloco à parede ocorre quando a força de atrito máxima (F_atmax) tem a mesma intensidade da força

elástica (F_e). F_atmax=F_e=μP=Kx  ---  x=μP/K=0,4.30/20  ---  x=0,6m  ---  R- C

51- As ranhuras tornam o piso mais áspero, aumentando o coeficiente de atrito.   

R- A

52- Se F=F_at, a resultante das força é nula e ao caixa se move em movimento retilíneo e uniforme  ---  R- D

53- Dados: m = 120 kg; g = 10 m/s²; m = 0,8; F/A= 30 N/cm²; N = P = 1.200 N  ---  para colocar a caixa em movimento o operador tem que vencer a força de atrito  ---  F_op = F_at = m N  ---  0,8 (1.200) = 960 N  ---  como ele está usando os dois braços, cada braço aplica então  ---   F = F_op/2=480 N  ---  F/A=30  ---  480/A=30  ---  A=16cm²  ---  uma das proteínas responsáveis pela contração das miofibrilas é a actina  ---  R- A

54- Como o movimento é uniforme, a resultante tangencial é nula  ---  assim, a componente de atrito tem a mesma intensidade da força motriz; e como o movimento é horizontal, a componente normal tem a mesma intensidade do peso  ---  dados: F_motriz = 2.000 N  ---   m = 200 kg  ---   g = 10 m/s²  ---  F_atc=F_motriz=2.000N  ---  N=P=mg=2.000N  ---  F_atc=2.000=μ_cN  ---  μ_c.2.000=2.000  ---

μ_c=1  ---  R- A

55- Dados  ---   x₁ = 2 cm; x₂ = 10 cm  ---  obseve as figuras abaixo onde foram colocadas as forças nas duas situações  --- 

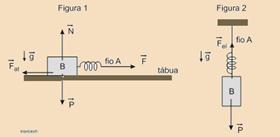
Na Figura 1, o bloco está na iminência de escorregar. A componente de atrito 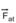  é máxima e, como o bloco ainda está em repouso, ela tem a mesma intensidade da força elástica 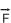.  Pela mesma razão, a componente normal  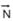tem a mesma intensidade que o peso 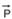do bloco  ---  sendo k a constante elástica da mola, m a massa do bloco e g a intensidade do campo gravitacional, temos  ---  N = P = m g  (I)  ---  F_at = F  Þ  m N = k x₁  (II)  ---  substituindo (I) em (II)  ---  m m g = k x₁   (III).

Na Figura 2, o bloco também está em repouso  ---  assim, a nova força elástica  equilibra o peso  ---  F_el = P  ---  k x₂ = m g (IV)  ---  substituindo (IV) em (III)  ---  m k ­x₂ = k x₁Þ  m =x₁/x₂=2/10  ---  m = 0,2  ---  R- B

56- Dados  ---  g = 10 m/s²  ---   m_e = 0,60  ---   m_c = 0,80  ---   m = 1.200 kg  ---   força que a pista exerce no veículo tem duas componentes  ---  normal 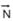 e  atrito  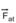 ---  supondo que a frenagem ocorra em pista horizontal, a componente normal  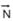 da força que a pista aplica no veículo tem intensidade igual à do seu peso  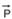 ---  N = P = m g = 12.000 N  ---   componente de atrito estático máxima  ---   F_atmax= m_e N = 0,8 (12.000)  ---   F_atmax = 9.600 N  ---  a componente de atrito cinético: F_atc  = m_c N = 0,6. (12.000)  ---   F_atc = 7.200 N  ---  R- D       

57- Na iminência de a caixa entrar em movimento, tem-se que as componentes horizontal e vertical da força resultante agindo sobre ela são nulas  ---  assim, para a componente horizontal, Fcos(θ) = F_{ate max}=μ_eN  ---  N e F_{ate max} denotam, respectivamente, os módulos da força normal e de atrito estático máxima nessa situação  ---  componente vertical  ---   N + Fsen(θ) = P  ---  combinando essas duas equações, obtém-se que F = μ_e P/[cos(θ) + μ_e sen(θ)]  ---  R- A

58- Na figura estão colocadas as forças que atuam sobre cada bloco  ---  o bloco P está em equilíbrio na vertical (não cai)  --- 

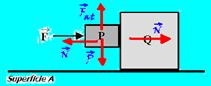
F_at=P  ---  μN=mg  ---  N=mg/μ (I)  ---  para que o bloco P não caia, ele deve se mover na horizontal com a mesma aceleração que a do bloco Q  ---  bloco P  ---  F – N=ma (II)  ---   bloco Q  ---  N=Ma (III)  ---  (II) com (III)  ---  F=(M + m).a (IV)  ---  (I) em (III)  --- 

Mg/μ=Ma  ---  a=mg/μM (V)  ---  (V) em (IV)  ---  F=(M + m).mg/μM  ---  F=mg/μM.(M + m)  ---  R- B

59- F_R=F_at=μN= μP= μmg=0,02.20.10  ---  F_R=4N  ---  F_R=ma  ---  4=20a  ---  a=0,2m/s²  ---  Torricelli  ---  V²=V_o² + 2.a.ΔS  --- 

0²=V_o² + 2.(-0,2).45  ---  V_o=√18≈4,2m/s  ---  V=V_o + at  ---  0=4,2 – 0,2t  ---  t≈21s  --- R- C

60-

01) Correta

02) Correta

04) Falsa  ---  constata-se experimentalmente que F_atemax>F_atc e que μ_e>μ_c, pois as reentrâncias e saliências das superfícies em contato estão mais encaixadas com o corpo em repouso, dificultando mais a movimentação.

08. Falsa  ---  F_at=μ.N  ---  μ=F_at (força-medida em N)/N (também força-medida  em N)  ---  o coeficiente de atrito é uma grandeza adimensional, ou seja, não tem unidades.

16. Falsa  ---  é a força de atrito estático máxima que é sempre maior que a força de atrito cinético.

Corretas: 01 e 02  ---  soma=03.

61-

Os freios antitravamento (ABS, anti-lock braking system) ajudam a parar melhor  ---  eles previnem o travamento das rodas e proporcionam uma distância de frenagem mais curta em superfícies escorregadias, evitando o descontrole do veículo  ---  ele mantém as rodas sempre na iminência de deslizar, aproveitando melhor o atrito estático máximo, que é maior que o atrito cinético (de deslizamento)  --- R- B.

62-

  Cálculo da aceleração de retardamento do carro    ---  V_o=54km/h/3,6=15m/s  ---  V=0 (pára)  ---  t=5s  ---  V= V_o + a.t  ---  0

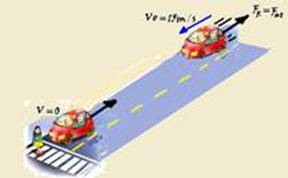
= 15 + a.5  ---  a= - 3m/s² (o sinal negativo de a significa que o carro está freando)  ---  em módulo  ---  a=3m/s²  ---  depois que ele acionou os freios a intensidade da força resultante sobre o carro é a própria força de atrito  ---  F_R=F_at  ---  m.a = μ.N  ---  m.a = μ.m.g  ---  3= μ.10  --- 

μ = 0,3  ---  R- A

63-

  Decompondo a força 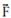 em sua componente horizontal  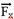e vertical  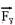  ---  F_x=Fcos37^o=50.0,8  ---  F_x=40N  ---  F_y=Fsen37^o=50.0,6  ---  F_y=30N  ---  colocando as forças peso  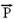(vertical e para baixo), a força normal 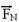(vertical e para cima) e

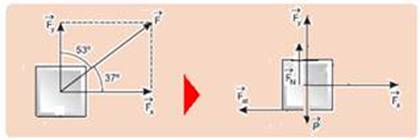
a força de atrito  (contrária ao movimento ou à sua tendência)  ---  equilíbrio na vertical  ---  P = F_y + F_N  ---  50=30 + F_N  ---  F_N=20N  ---  F_at=μF_N=0,6.20  ---  F_at=12N  ---  na horizontal existe força resultante, pois F_R=F_x – F_at  ---  F_R= 40 – 12  ---  F_R=28N  ---  F_R=m.a  ---  28=5.a  ---  a=5,6m/s²  ---  R- D

64-

  Colocando todas as forças (figura) que influem no movimento ou na sua tendência  --- força de atrito  --- 

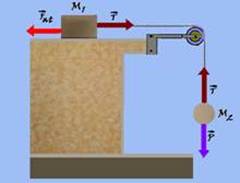
F_at=μN=μM₁.g  ---  F_at=μ.10.10  ---  F_at=100μ  ---  como o sistema está em equilíbrio estático (repouso) a força resultante sobre cada corpo é nula  ---  F_at=T  ---  100μ=T (I)  ---  como o bloco M₂ também está em repouso  ---  T=P=M₂.g=5.10  ---  T=50N II)  ---  substituindo (II) em (I)  ---  100μ=50  ---  μ=0,5  ---  R- C

65-

 a) As forças que agem sobre o conjunto imã-grampo são  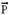---   – força peso, vertical e para baixo, aplicada sobre o conjunto

pela Terra  ---   - força de tração no fio, vertical e para baixo, aplicada sobre o conjunto pela massa M pendurada  ---  - força de atrito, trocada entre o conjunto  e a parede da geladeira, vertical e para cima, contrária ao movimento ou à sua tendência  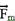---   -  força magnética, horizontal e que atrai o conjunto para a esquerda, é de atração magnética entre o imã e a parede da geladeira  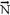---   – força normal, horizontal e para a direita, reação da parede da geladeira sobre o conjunto.

b) Se o conjunto não deve cair a força resultante sobre ele tanto na vertical como na horizontal deve ser nula  ---  equilíbrio na vertical  ---

F_at=P + T  ---  P=m_og  ---  T=Mg  ---  F_at=μ_eN  ---  μ_eN = m_og + Mg (I)  ---  equilíbrio na horizontal  ---  F_M=N (II)  ---  (II0 em (I)  ---  μ_eF_M = m_og + Mg  ---  Mg = μ_eF_M – m_og  ---  M= (μ_eF_M – m_og)/g ou M= μ_eF_M/g - m_o ---  para esse valor de M o conjunto está na iminência de cair  ---  para qualquer valor de M menor que esse, o conjunto não cai.