Força Centrípeta (Forças no movimento circular em trajetórias curvas)

Forças no movimento circular em trajetórias curvas Exercícios

01-(PUC-RJ) Um carro de massa m = 1000 kg realiza uma curva de raio R = 20 m com uma velocidade angular w = 10 rad/s.

 A força centrípeta atuando no carro em newtons vale:

a) 2,0 10⁶.                b) 3,0 10⁶ .                 c) 4,0 10⁶.                  d) 2,0 10⁵.                   e) 4,0 10⁵.

02-(PUC-SP) Um automóvel percorre uma curva circular e horizontal de raio 50 m a 54 km/h. Adote g = 10 m/s². O mínimo coeficiente de atrito estático entre o asfalto e os pneus que permite a esse automóvel fazer a curva sem derrapar é

a) 0,25                    b) 0,27                    c) 0,45                    d) 0,50                       e) 0,54

03-(UFRS) A figura a seguir representa um pêndulo cônico ideal que consiste em uma pequena esfera suspensa a um ponto fixo por meio de um cordão de massa desprezível.

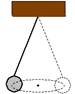
Para um observador inercial, o período de rotação da esfera, em sua órbita circular, é constante. Para o mesmo observador, a resultante das forças exercidas sobre a esfera aponta

a) verticalmente para cima.      b) verticalmente para baixo.      c) tangencialmente no sentido do movimento.

d) para o ponto fixo.      e) para o centro da órbita.

(FGV-SP) Texto para as questões de números 04 e 05

 Vendedores aproveitam-se da morosidade do trânsito para vender amendoins, mantidos sempre aquecidos em uma bandeja perfurada encaixada no topo de um balde de alumínio; dentro do balde, uma lata de leite em pó, vazada por cortes laterais, contém carvão em brasa. Quando o carvão está por se acabar, nova quantidade é reposta. A lata de leite é enganchada a uma haste de metal e o conjunto é girado vigorosamente sob um plano vertical por alguns segundos , reavivando a chama.

04-(FGV-SP) Considere um braseiro (balde com furos e carvão em seu interior) em movimento circular  de raio 80cm para ativar as brasas.

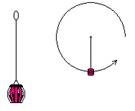
 Mantendo esse movimento circular, determine a menor velocidade que a lata deve possuir no ponto mais alto de sua trajetória para que o carvão não caia da lata:

a) Ö2                     b) 2                     c) 2Ö2                       d) 4                       e) 4Ö2

05-(FGV-SP) Com relação ao exercício anterior, no momento em que o braseiro atinge o ponto mais baixo de sua trajetória, considerando que ele descreve um movimento no sentido anti-horário e que a trajetória é percorrida com velocidade constante, dos vetores indicados, aquele que mais se aproxima da direção e sentido da força resultante sobre a lata é

06-(UNIFESP-SP) A trajetória de uma partícula, representada na figura, é um arco de circunferência de raio r = 2,0 m, percorrido com velocidade de módulo constante, v = 3,0 m/s.

O módulo da aceleração vetorial dessa partícula nesse trecho, em m/s², é

a) zero.               b) 1,5.                  c) 3,0.                d) 4,5.                  e) impossível de ser calculado.

07-(UFMG-MG) Devido a um congestionamento aéreo, o avião em que Flávia viajava permaneceu voando em uma trajetória horizontal e circular, com velocidade de módulo constante.

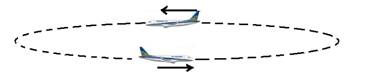
Considerando-se essas informações, é CORRETO afirmar que, em certo ponto da trajetória, a resultante das forças que atuam no avião é

a) horizontal.          b) vertical, para baixo.          c) vertical, para cima.          d) nula.

08-(ITA-SP) Para um avião executar uma curva nivelada (sem subir ou descer) e equilibrada, o piloto deve incliná-lo com respeito à horizontal (à maneira de um ciclista em uma curva), de um ângulo a. Se a= 60°, a  velocidade da aeronave é 100 m/s e a aceleração local da gravidade é 9,5 m/s2, qual é aproximadamente o raio de curvatura?

a) 600 m.            b) 750 m.            c) 200 m.             d) 350 m.              e) 1000 m.

09-(UNICAMP-SP) Um pêndulo cônico é formado por um fio de massa desprezível e comprimento L = 1,25 m, que suporta uma massa m = 0,5 kg na sua extremidade inferior.

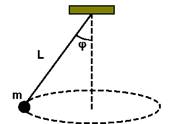
A extremidade superior do fio é presa ao teto, conforme ilustra a figura a seguir. Quando o pêndulo oscila, a massa m executa um movimento circular uniforme num plano horizontal, e o ângulo que o fio forma com a vertical é j = 60°.

a) Qual é a tensão no fio?

b) Qual é a velocidade angular da massa? Se for necessário, use: sen 60°= 0,87, cos 60°= 0,5.

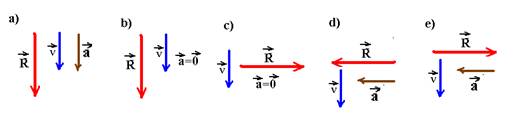
10- (ITA) Uma mosca em movimento uniforme descreve a trajetória curva indicada abaixo:

                                               

 Quanto à intensidade da força resultante na mosca, podemos afirmar:

      a) é nula, pois o movimento é uniforme         b) é constante, pois o módulo de sua velocidade é constante;

      c) está diminuindo           d) está aumentando                   e) n.d.a.

11 (FUVEST) Um carro percorre uma pista curva superelevada (tg q = 0,20) de 200m de raio. Desprezando o atrito, qual a velocidade máxima sem risco de derrapagem? Adote g = 10m/s²

a) 60km/h          b) 72km/h          c) 80km/h           d) 40km/h           e) 48km/h

12-(PUC-SP)

A figura representa em plano vertical um trecho dos trilhos de uma montanha russa na qual um carrinho está prestes a realizar uma curva. Despreze atritos, considere a massa total dos ocupantes e do carrinho igual a 500 kg e a máxima velocidade com que o carrinho consegue realizar a curva sem perder contato com os trilhos igual a 36 km/h. O raio da curva, considerada circular, é, em metros, igual a: (g=10m/s²)

a) 3,6                       b) 18                      c) 1,0                      d) 6,0                       e) 10

13-(Ufrrj 2005) Foi que ele viu Juliana na roda com João

Uma rosa e um sorvete na mão

Juliana seu sonho, uma ilusão

Juliana e o amigo João

            GIL, Gilberto. "Domingo no Parque".

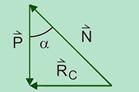
A roda citada no texto é conhecida como RODA-GIGANTE, um brinquedo de parques de diversões no qual atuam algumas forças, como a força centrípeta.

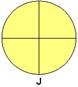
Considere:

- o movimento uniforme; - o atrito desprezível; - aceleração da gravidade local de 10 m/s²; - massa da Juliana 50 kg;

- raio da roda-gigante 2 metros; - velocidade escalar constante, com que a roda está girando, 36 km/h.

Calcule a intensidade da reação normal vertical que a cadeira exerce sobre Juliana quando a mesma se encontrar na posição indicado pelo ponto J.

14-(UFB)A figura representa a seção vertical de um trecho de rodovia. Os raios de curvatura dos pontos A e B são iguais e valem 100m e o trecho que contém o ponto C é horizontal.

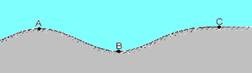
Um automóvel de massa 2.10³ kg  percorre a rodovia com velocidade escalar constante de 36km/h.. Sendo N_A, N_B e N_C a reação normal da rodovia sobre o carro nos pontos A, B e C, respectivamente, determine suas intensidades.

15-(UFSC) Um avião descreve uma curva em trajetória circular com velocidade escalar constante, num plano horizontal, conforme está representado na figura, onde F é a força de sustentação, perpendicular às asas; P é a força peso; a é o ângulo de inclinação das asas em relação ao plano horizontal; R é o raio de trajetória.

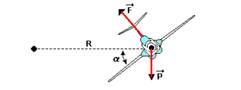
 São conhecidos os valores: a = 45°,  R =1000 metros;  massa do avião = 10000 kg, g=10m/s².

 Assinale a(s) proposição(ões) CORRETA(S),  indicando sua soma econsiderando, para efeito de cálculos, apenas as forças indicadas na figura.

01. Se o avião realiza movimento circular uniforme, a resultante das forças que atuam sobre ele é nula.

02. Se o avião descreve uma trajetória curvilínea, a resultante das forças externas que atuam sobre ele é, necessariamente, diferente de zero.

04. A resultante centrípeta é, em cada ponto da trajetória, a resultante das forças externas que atuam no avião, na direção do raio da trajetória.

08. A resultante centrípeta sobre o avião tem intensidade igual a 100000N.

16. A velocidade do avião tem valor igual a 360 km/h.

32. A força resultante que atua sobre o avião não depende do ângulo de inclinação das asas em

relação ao plano horizontal.

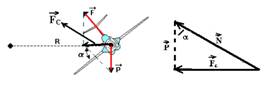
16-(Ufpb) Após a ocorrência de um pequeno acidente, um astronauta necessita fazer um reparo na parte externa de sua espaçonave, que possui um formato cilíndrico com um raio de 10m. Ressalte-se que a nave espacial está girando em torno de seu próprio eixo, dando uma volta completa a cada 20 segundos, e o astronauta precisa se segurar na mesma para realizar o conserto e não ser lançado no espaço. Determine a força mínima, em newtons, para que o astronauta de 70kg se mantenha preso à espaçonave.

17- (FUVEST-SP) Uma estação espacial, construída em forma cilíndrica, foi projetada para contornar a ausência de gravidade no espaço. A figura mostra, de maneira simplificada, a secção reta dessa estação, que possui dois andares.

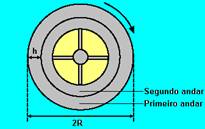
Para simular a gravidade, a estação deve girar em torno do seu eixo com certa velocidade angular. Se o raio externo da estação é R,

a) deduza a velocidade angular W com que a estação deve girar para que um astronauta, em repouso no primeiro andar e a uma distância R do eixo da estação, fique sujeito a uma aceleração igual a g.

b) Suponha que o astronauta vá para o segundo andar, a uma distância h do piso do andar anterior. Calcule o peso do astronauta nessa posição e compare com o seu peso quando estava no primeiro andar. O peso aumenta, diminui ou permanece inalterado ?

18-(UNESP-SP) Uma espaçonave de massa m gira em torno da Terra com velocidade constante, em uma órbita circular de raio R. A força centrípeta sobre a nave é 1,5 GmM/R², onde G é a constante de gravitação universal e M a massa da Terra.

a) Desenhe a trajetória dessa nave. Em um ponto de sua trajetória, desenhe e identifique os vetores velocidade 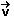 e aceleração centrípeta  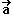da nave.

b) Determine, em função de M, G e R, os módulos da aceleração centrípeta e da velocidade da nave.

19-(FUVEST) – Um restaurante é montado numa plataforma que gira com velocidade angular constante W= p/1800 radianos/segundo. Um freguês, de massa M = 50kg, senta-se no balcão localizando-se a 20 metros do eixo de rotação, toma sua refeição e sai no mesmo ponto de entrada.

a) qual o tempo mínimo de permanência do freguês na plataforma?

b) Qual a intensidade da força centrípeta sobre o freguês enquanto toma a sua

refeição?

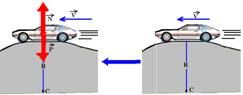
20-(Uff-RJ) A figura 1 mostra uma rampa de skate constituída de um trecho curvo que corresponde a um quarto de circunferência de raio R, e de um trecho plano horizontal.

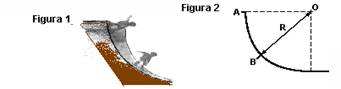
Os dois pontos A e B , indicados no esquema da figura 2, se encontram localizados, respectivamente, no topo e no meio do trecho curvo da pista de skate.

Para a análise desse movimento o jovem, junto com sua prancha de skate, pode ser tratado como uma partícula de massa total m. Admita, também, que os efeitos de forças dissipativas sobre o movimento dessa partícula possam ser ignorados.

a) Indique e identifique, na figura 2, as forças que atuam sobre a partícula quando ela se encontra no ponto A e quando se encontra no ponto B.

b) Obtenha, em função de R, m e g (aceleração da gravidade local) o módulo da força exercida pela rampa sobre a partícula, quando essa se encontra no ponto B.

21-(UFMG-MG) Durante uma aula de Física, o Professor Raimundo faz uma demonstração com um pêndulo cônico. Esse pêndulo consiste em uma pequena esfera pendurada na extremidade de um fio, como mostrado nesta figura:

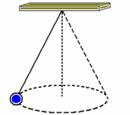
Nesse pêndulo, a esfera descreve um movimento circular com velocidade de módulo constante, em um plano horizontal, situado a 1,6 m abaixo do ponto em que o fio está preso ao teto. A massa da esfera é 0,40 kg, o raio de sua trajetória é 1,2 m e o comprimento do fio é 2,0 m. Considere a massa do fio desprezível. Despreze, também, qualquer tipo de atrito.

Com base nessas informações:

a) DESENHE e NOMEIE, na figura, as forças que atuam na esfera. RESPONDA: Quais são os agentes que exercem essas forças?

b) CALCULE a tensão no fio.

22-(CESUPA-PA) Um corpo de massa 500 g gira num plano horizontal em torno de um ponto fixo, preso à extremidade de um fio de 1 m de comprimento e massa desprezível.

 (considere 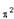= 10).

Se o corpo efetua 60 voltas completas a cada meio minuto, então a força de tração exercida pelo fio, em newtons, é: (considere 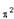= 10).
a) 10.                     b) 80.                        c) 30.                       d) 160.                     e) 50.

23-(CESESP-PE) Um caminhão transporta em sua carroceria uma carga de 2,0 toneladas. Determine, em newtons, a intensidade da força normal exercida pela carga sobre o piso da carroceria, quando o veículo, a 30 m/s, passa pelo ponto mais baixo de uma depressão com 300 m de raio. (g = 10 m/s/²)

24-(Mackenzie-SP) A figura representa a seção vertical de um trecho de rodovia. Os raios de curvatura dos pontos A e B são iguais e o trecho que contém o ponto C é horizontal. Um automóvel percorre a rodovia com velocidade escalar constante. Sendo N_A, N_B e N_C a reação normal da rodovia sobre o carro nos pontos A, B e C, respectivamente podemos dizer que:

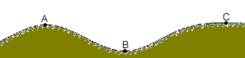
a) N_B > N_A > N_C.           b) N_B > N_C > N_A.          c) N_C > N_B > N_A.          d) N_A > N_B > N_C.          e) N_A = N_C = N_B.

25-(UNESP-SP) Uma partícula de massa m descreve uma trajetória circular com movimento uniforme, no sentido horário, como mostra a figura.

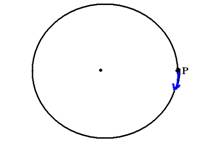
Qual dos seguintes conjuntos de vetores representa a força resultante  atuando na partícula, a velocidade 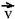 e a aceleração  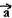da partícula, no ponto P indicado na figura?

26- (UEL-PR) Um carro consegue fazer uma curva plana e horizontal, de raio 100 m, com velocidade constante de 20 m/s. Sendo g=10m/s², o mínimo coeficiente de atrito estático entre os pneus e a pista deve ser:
a) 0,20        b) 0,25        c) 0,30        d) 0,35        e) 0,40

27-(UNESP-SP) A figura 1 mostra uma esfera de massa m, em repouso, suspensa por um fio inextensível. A figura 2 representa o mesmo conjunto, oscilando como um pêndulo, no instante em que a esfera passa por um ponto mais baixo de sua trajetória.

Explique para qual figura a tração no fio é maior.

28-(Ufrrj-RJ) Um motoqueiro deseja realizar uma manobra radical num "globo da morte" (gaiola esférica) de 4,9m de raio.

Para que o motoqueiro efetue um "looping" (uma curva completa no plano vertical) sem cair, o módulo da velocidade mínima no ponto mais alto da curva deve ser de

Dado: Considere g=10m/s².

a) 0,49m/s.               b) 3,5m/s.                 c) 7m/s.                   d) 49m/s.                  e) 70m/s.

29-(UFU-MG) Em uma corrida de automóveis, um dos trechos da pista é um pequeno morro com a forma de um arco de circunferência de raio R, conforme indicado na figura a seguir.

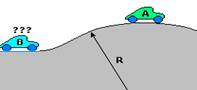
O carro A, que segue na frente do carro B, ao passar pelo ponto mais alto do morro fica na iminência de perder o contato com o solo. O piloto do carro B observa o carro A quase perdendo o contato com o solo e fica impressionado com a habilidade do piloto do carro A. Assim, o piloto do carro B, sabendo que seu carro tem uma massa 10% maior do que a massa do carro A, tenta fazer o mesmo, isto é, passar pelo ponto mais alto do morro da pista também na iminência de perder o seu contato com o solo. Para que isso ocorra, a velocidade do carro B, no topo do morro, deve ser:

a) 10% menor do que a velocidade de A no topo do morro.      b) 10% maior do que a velocidade de A no topo do morro.

c) 20% maior do que a velocidade de A no topo do morro.      d) igual à velocidade de A no topo do morro.

30-(UFV-MG) Um corpo de massa M (circulo preto), suspenso por um fio inextensível e de massa desprezível, está ligado a um dinamômetro através de uma roldana conforme ilustrado na figura (I) adiante.

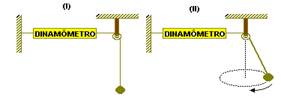
Se o corpo é posto a girar com uma freqüência angular constante, conforme ilustrado na figura (II) acima, e desprezando qualquer tipo de atrito, é CORRETO afirmar que, comparada com a situação (I), o valor da leitura do dinamômetro:

a) será menor.                     b) não se altera                      c) será maior.                     d) será nulo

31-(FUVEST-SP-09)  Um acrobata, de massa MA = 60 kg, quer realizar uma apresentação em que, segurando uma corda suspensa em um ponto Q fixo, pretende descrever um círculo de raio R = 4,9 m, de tal forma que a corda mantenha um ângulo de 45° com a vertical. Visando garantir sua total segurança, há uma recomendação pela qual essa corda deva ser capaz de suportar uma tensão de, no mínimo, três vezes o valor da tensão a que é submetida durante a apresentação. Para testar a corda, com ela parada e na vertical, é pendurado em sua extremidade um bloco de massa M_o, calculada de tal forma que a tensão na corda atenda às condições mínimas estabelecidas pela recomendação de segurança.

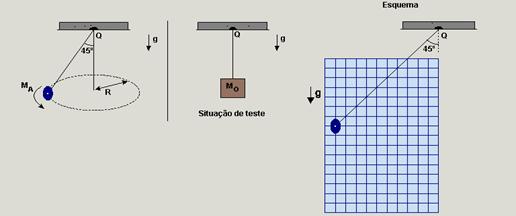
Nessa situação:

a) Represente no esquema a direção e o sentido das forças que agem sobre o acrobata, durante sua apresentação, identificando-as, por meio de um desenho em escala.

b) Estime o tempo t_A, em segundos, que o acrobata leva para dar uma volta completa em sua órbita circular.

c) Estime o valor da massa M_o, em kg, que deve ser utilizada para realizar o teste de segurança.

NOTE E ADOTE: Força centrípeta F_c = m v²/R

Adote g=10m/s²

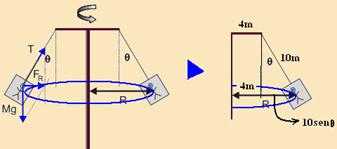
32-(PUC-RJ-09)  Um brinquedo de parque de diversões consiste (veja as figuras a seguir) de um eixo vertical girante, duas cabines e um suporte para os cabos que ligam o eixo às cabines. O suporte é uma forte barra horizontal de aço, de L = 8,0 m de comprimento, colocada de modo simétrico para poder sustentar as cabines. Cada cabo mede d = 10 m.

Quando as pessoas entram nas cabines, o eixo se põe a girar e as cabines se inclinam formando um ângulo θ com a vertical. O movimento das cabines é circular uniforme, ambos de raio R. Considere a massa total da cabine e passageiro como M = 1000 kg.

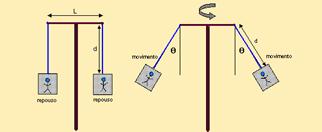
Suponha que θ = 30°. Considere g = 10 m/s² para a aceleração gravitacional e despreze todos os efeitos de resistência do ar.

a) Desenhe na figura anterior o raio R de rotação, para a trajetória da cabine do lado direito, e calcule seu valor.

b) Desenhe na figura anterior as forças agindo sobre a cabine do lado esquerdo. Qual a direção e o sentido da força resultante F_R sobre esta cabine?

c) Sabendo que as forças verticais sobre a cabine se cancelam, calcule a tensão no cabo que sustenta a cabine.

d) Qual o valor da força centrípeta agindo sobre a cabine?

33-(UDESC-SC-09)  Na figura a seguir, o sul-africano Mark Shuttleworth, que entrou para história como o segundo turista espacial, depois do empresário norte-americano Dennis Tito, "flutua" a bordo da Estação Espacial Internacional que se  encontra

em órbita baixa (entre 350 km e 460 km da Terra). Sobre Mark, é correto afirmar:

 a)  tem a mesma aceleração da Estação Espacial Internacional.                 b)  não tem peso nessa órbita. 

c)  tem o poder da levitação.                                                                        d)  permanece flutuando devido à inércia. 

e)  tem velocidade menor que a da Estação Espacial Internacional. 

34-(UEL-PR-09)  Considere um satélite artificial que tenha o período de revolução igual ao período de rotação da Terra (satélite

 geossíncrono). É CORRETO afirmar que um objeto de massa m dentro de um satélite desse tipo:

a) Fica sem peso, pois flutua dentro do satélite se ficar solto. 

b) Apresenta uma aceleração centrípeta que tem o mesmo módulo da aceleração gravitacional do satélite. 

c) Não sente nenhuma aceleração da gravidade, pois flutua dentro do satélite se ficar solto. 

d) Fica sem peso porque dentro do satélite não há atmosfera. 

e) Não apresenta força agindo sobre ele, uma vez que o satélite está estacionário em relação à Terra. 

35-(UNESP-SP-2010)  Curvas com ligeiras inclinações em circuitos automobilísticos são indicadas para aumentar a segurança do carro a altas velocidades, como, por exemplo, no Talladega Superspeedway, um circuito utilizado para corridas promovidas pela NASCAR (National Association for Stock Car Auto Racing). Considere um carro como sendo um ponto material percorrendo uma pista circular, de centro C, inclinada de um ângulo 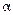 e com raio R, constantes, como mostra a figura, que apresenta a frente do carro em um dos trechos da pista.

Se a velocidade do carro tem módulo constante, é correto afirmar que o carro

a) não possui aceleração vetorial. 

b) possui aceleração com módulo variável, direção radial e no sentido para o ponto C. 

c) possui aceleração com módulo variável e tangente à trajetória circular. 

d) possui aceleração com módulo constante, direção radial e no sentido para o ponto C. 

e) possui aceleração com módulo constante e tangente à trajetória circular. 

36-(PUC-SP-010)  Um automóvel de massa 800 kg, dirigido por um motorista de massa igual a 60 kg, passa pela parte mais baixa de uma depressão de raio = 20 m com velocidade escalar de 72 km/h. Nesse momento, a intensidade da força de reação que a pista

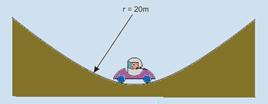
aplica no veículo é: (Adote g = 10m/s²).

a) 231.512 N                   b) 215.360 N                            c) 1.800 N                           d) 25.800 N                             e) 24.000 N 

37-(UFC-CE-010)  Uma partícula de massa m está pendurada no teto através de um fio ideal de comprimento l. Determine o período, sabendo que a partícula realiza um movimento circular uniforme horizontal de raio a, onde l > a.

Despreze atritos e considere a aceleração da gravidade local constante e de módulo igual a g. A seguir, assinale a alternativa que apresenta corretamente esse período.

38-(UFSC-SC-010)  Rotor é um brinquedo que pode ser visto em parques de diversões.Consiste em um grande cilindro de raio R que pode girar em torno de seu eixo vertical central. Após a entrada das pessoas no rotor, elas se encostam nas suas paredes e este começa a girar. O rotor aumenta sua velocidade de rotação até que as pessoas atinjam uma velocidade v, quando, então, o piso é retirado. As pessoas ficam suspensas, como se estivessem “ligadas” à parede interna do cilindro enquanto o mesmo está girando, sem nenhum apoio debaixo dos pés e vendo um buraco abaixo delas.

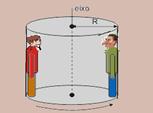
Em relação à situação descrita, é CORRETO afirmar que:

01) a força normal, ou seja, a força que a parede faz sobre uma pessoa encostada na parede do rotor em movimento, é uma força centrípeta. 

02) se duas pessoas dentro do rotor tiverem massas diferentes, aquela que tiver maior massa será a que terá maior chance de deslizar e cair no buraco abaixo de seus pés. 

04) o coeficiente de atrito estático entre a superfície do rotor e as roupas de cada pessoa dentro dele deve ser maior ou igual a gR/V². 

08) o coeficiente de atrito estático entre a superfície do rotor e as roupas de cada pessoa dentro dele é proporcional ao raio do rotor. 

16) o coeficiente de atrito estático entre a superfície do rotor e as roupas de cada pessoa dentro dele é proporcional à velocidade v do rotor. 

39-(UFPR-PR-010)  Convidado para substituir Felipe Massa, acidentado nos treinos para o grande prêmio da Hungria, o piloto alemão Michael Schumacker desistiu após a realização de alguns treinos, alegando que seu pescoço doía, como consequência de um acidente sofrido alguns meses antes, e que a dor estava sendo intensificada pelos treinos. A razão disso é que, ao realizar uma

 curva, o piloto deve exercer uma força sobre a sua cabeça, procurando mantê-la alinhada com a vertical.

Considerando que a massa da cabeça de um piloto mais o capacete seja de 6,0 kg e que o carro esteja fazendo uma curva de raio igual a 72 m a uma velocidade de 216 km/h, assinale a alternativa correta para a massa que, sujeita à aceleração da gravidade, dá uma força de mesmo módulo.

a) 20 kg.                          b) 30 kg.                            c) 40 kg.                                  d) 50 kg.                        e) 60 kg. 

 40-(UFOP-MG-010)  Uma estação espacial é projetada como sendo um cilindro de raio r, que gira em seu eixo com velocidade angular constante W, de modo a produzir uma sensação de gravidade de 1g = 9,8 m/s² nos pés de uma pessoa que está no interior

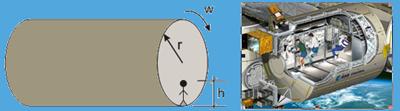
 da estação. Admitindo-se que os seus habitantes têm uma altura média de h = 2 m, qual deve ser o raio mínimo r da estação, de modo que a variação da gravidade sentida entre os pés e a cabeça seja inferior a 1% de g?

               

41-(UNESP-SP-010)  Algumas montanhas-russas possuem inversões, sendo uma delas denominada loop, na qual o carro, após uma descida íngreme, faz uma volta completa na vertical. Nesses brinquedos, os carros são erguidos e soltos no topo da montanha

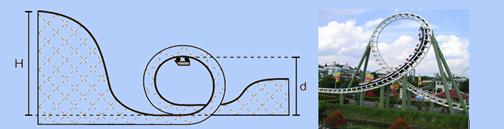
mais alta para adquirirem velocidade. Parte da energia potencial se transforma em energia cinética, permitindo que os carros completem o percurso, ou parte dele. Parte da energia cinética é novamente transformada em energia potencial enquanto o carro se move novamente para o segundo pico e assim sucessivamente.

Numa montanha-russa hipotética, cujo perfil é apresentado, o carro (com os passageiros), com massa total de 1 000 kg, é solto de uma altura H = 30 m (topo da montanha mais alta) acima da base de um loop circular com diâmetro d = 20 m. Supondo que o atrito entre o carro e os trilhos é desprezível, determine a aceleração do carro e a força vertical que o trilho exerce sobre o carro quando este passa pelo ponto mais alto do loop. Considere g = 10 m/s².

42-(PUC-SP-011) Considere que, numa montanha russa de um parque de diversões, os carrinhos do brinquedo, de massa total ,

passem pelo ponto mais alto do loop, de tal forma que a intensidade da reação normal nesse instante seja nula. Adotando como o raio do loop e a aceleração da gravidade local, podemos afirmar que a velocidade e a aceleração centrípeta sobre os carrinhos na situação considerada valem, respectivamente,

a) √mrg e mr                    b) √rg e mr                      c) √rg e mr/g                     d) √rg e nula                        e) √rg e g

43-(UFSC-SC-011) Um pêndulo, constituído de uma massa de 0,5 kg presa à extremidade de uma corda, inextensível e de massa desprezível, de 1 m de comprimento, é posto a girar em um círculo vertical, passando pelos pontos A, B, C e D, assinalados na

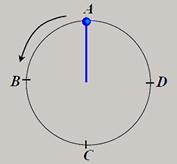
figura. Desconsidere qualquer atrito do pêndulo com o ar entre o fio e o eixo de suspensão.

Em relação ao exposto, assinale a(s) proposição(ões) CORRETA(S).

01. O módulo da força de tensão na corda no ponto C é igual ao peso.

02. No ponto B atuam três forças sobre a pedra: o peso, a força centrípeta e a força de tensão da corda.

04. A menor velocidade que a massa pode ter no ponto C de modo a descrever a trajetória circular completa é de 50 m/s.

08. A menor energia cinética que a massa pode ter no ponto A de modo a descrever a trajetória circular completa é 2,5 J.

16. Se a velocidade da massa no ponto B for de 30 m/s, a tensão na corda, nesta posição, será de 15 N.

32. Se a velocidade da massa no ponto B for de 30 m/s, a força resultante sobre a massa, nesta posição, será menor do que 7,5 N.

44-(UFAL-AL-011) Um carro passa por uma elevação na pista com velocidade de módulo constante e igual a 10 km/h. A elevação corresponde a um arco de uma circunferência de raio R = 5 m, centrada no ponto O (ver figura).

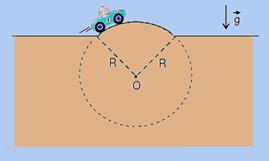
Considerando o carro como uma partícula material, qual a sua aceleração centrípeta, em km/h², sobre a elevação?

a) 2                                      b) 4                                      c) 200                                      d) 400                                         e) 20.000

45-(CPS-SP-011) Salto de penhasco é um esporte que consiste em saltar de uma plataforma elevada, em direção à água,

realizando movimentos estéticos durante a queda. O saltador é avaliado nos seguintes aspectos: criatividade, destreza, rigorosa execução do salto previsto, simetria, cadência dos movimentos e entrada na água. Considere que um atleta salte de uma plataforma e realize 4 rotações completas durante a sua apresentação, entrando na água 2 segundos após o salto, quando termina a quarta rotação. Sabendo que a velocidade angular para a realização de n rotações é calculada pela expressão

em que n é o número de rotações e Δt é o tempo em segundos, assinale a alternativa que representa a velocidade angular das rotações desse atleta, em graus por segundo.

a) 360                                    b) 720                                       c) 900                                d) 1 080                                        e) 1 440

46-(UNIOESTE-PR-012)

 Na Fórmula Indy utilizam-se circuitos ovais com pistas super elevadas, isto é: inclinadas por um certo ângulo θ com

 

relação à horizontal. Esta geometria garante que para uma curva com determinado raio de curvatura R_c exista uma velocidade máxima de segurança V_max com a qual um veículo não desgarra do asfalto, mesmo que seus pneus percam o atrito com a pista. Admitindo que em certo ponto da pista onde os veículos podem atingir V_max = 360 km/h a inclinação seja θ = 30°, qual será a melhor aproximação para o raio de curvatura R_c associado a esta região? Admita g = 10 m/s².

A. R_c = 577 m.        B. R_c = 1154 m.           C. R_c = 1414 m.                D. R_c = 1732 m.               E. R_c = 2000 m.

 47-(UFSM-RS-012)

A figura representa dois atletas numa corrida, percorrendo uma curva circular, cada um em uma raia. Eles desenvolvem

velocidades lineares com módulos iguais e constantes, num referencial fixo no solo. Atendendo à informação dada, assinale a resposta correta.

a) Em modulo, a aceleração centrípeta de A é maior do que a aceleração centrípeta de B.

b) Em modulo, as velocidades angulares de A e B são iguais.

c) A poderia acompanhar B se a velocidade angular de A fosse maior do que a de B, em modulo.

d) Se as massas dos corredores são iguais, a força centrípeta sobre B é maior do que a força centrípeta sobre A, em modulo.

e) Se A e B estivessem correndo na mesma raia, as forças centrípetas teriam módulos iguais, independentemente das massas.

48-(UFF-SP-012)

Uma criança se balança de um balanço, como representado esquematicamente na figura ao lado. Assinale a alternativa que melhor

representa a aceleração  da criança no instante em que ela passa pelo ponto mais baixo da trajetória.

 Resoluções:

01- F_C=m.W².R  ---  F_C=1.000.(10)².20  ---  F_C=2.10⁶N  R- A

02- A força de atrito estático será máxima quando o carro estiver na iminência  de escorregar para fora da pista e nesse caso F_atemáximo=m_eN=m_eP=m_emg  ---  F_c=F_atmáx  ---  mV²/R=m_emg  ---  , que é a máxima velocidade com que ele consegue fazer a curva sem derrapar  ---  V=Öm.R.g  ---  (15)²=(Öm.50.10)²  ---  225=500m  ---  m=0,45  R-C

03- R- E (vide teoria)

04- A velocidade mínima para que o carvão não caia ocorrerá quando a força de compressão no ponto superior for nula, ou seja, quando N=0  ---  F_C=P + N  ---  F_C=P + 0  ---  F_C=P  ---  m.V²/R=m.g   ---  V=Ö(R.g)  ---  V=Ö0,8.10  ---  V=Ö8=2Ö2m/s  R- C

05- R-A (vide teoria)

06- a_C=V²/R  ---  a_C=9/2  ---  a_C=4,5m/s²  R- D

07- Como a curva é horizontal, a força resultante centrípeta que é radial e dirigida para o centro da circunferência deverá ser também horizontal. R- A

08- Colocando as forças:

a é o ângulo de inclinação das asas em relação ao plano horizontal  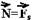---   é a força de sustentação aplicada pelo ar e que é perpendicular às asas  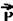---   é o peso.

tga=cateto oposto/cateto adjacente  ---  tga=F_c/P  ---  tga=(m.V²/R)/mg 

   ---   substituindo os valores  ---  100=Ö(R.9,5.Ö3)  ---  10.000=R.9,5.1,7  ---  R=10.000/16,15  ---  R=619,2m  R- A

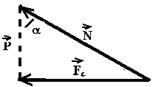
09- Colocando as forças:

a) P=m.g  ---  P=0,5.10  ---  P=5N  ---  Da figura da direita  ---   cosj=P/T  ---  0,5=5/T  ---  T=10N

b) Da figura da direita - tgj=F_c/P  ---  tgj=(mV²/R)/mg  ---  tgj=V²/Rg   ---  R=Lsenj  --- tgj=V²/L.senj.g  --- em função da velocidade angular W=V/R  ---  V=W.R  ---  senj/cosj=W².R²/R.g  ---  senj/cosj=W².R/.g  ---  senj/cosj=W².Lsenj/.g  --- 

     ---   substituindo os valores  ---  W=Ö(10/1,25.0,5)  ---  W=Ö16  ---  W=4rad/s

10- Sendo o movimento circular a força resultante sobre a mosca é a centrípeta de direção radial, sentido para o centro da circunferência e intensidade Fc₌m_.V²/R. Como m e V são constantes,F_c e R são inversamente proporcionais, ou seja, quanto menor é o raio R, maior será a intensidade da força resultante centrípeta F_c. R- D 

11- Colocando as forças:

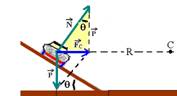
No triângulo hachurado  ---  tgq=cateto oposto/cateto adjacente  ---  tgq=F_C/P  ---  tgq=(mV²/R)/mg  ---  V²=R.g.tgq

V=ÖR.g.tgq  ---  máxima velocidade que o carro deve ter para efetuar a curva sem atrito  ---  V=Ö200.10.0,2  --- 

V=20m/s que dividido por 3,6 nos fornece V=72km/h  R- B

12- A máxima velocidade com que o carro consegue realizar a curva sem perder contato com o solo ocorre quando a força de

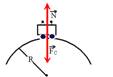
compressão 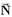 entre os pneus do carro e o solo é nula, ou seja, N=0  ---  F_C=P-N  ---  mV²/R=mg – 0  ---  V²/R=g  --- 

V=ÖR.g   ---  10=ÖR.10  ---  (10)²=(ÖR.10)²  ---  100=10R    ---  R=10m  R- C

13- a força resultante centrípeta 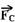 , que é dirigida sempre para o centro da circunferência, no caso, para

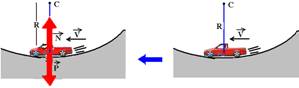
cima, é a diferença vetorial entr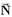e  e  , de intensidade  ---  F_C=N – P  ---   m.V²/R= N – m.g  ---  N=m.g + mV²/R

N=50.10 + 50.100/2  ---  N=3.10³N

14- Ponto A - lombada

A força resultante centrípeta que é sempre dirigida para o centro da circunferência que é para baixo, ou seja, FC=mV²/R    --- 

P – N=mV²/R   ---   mg – N = mV²/R  ---   N=2.10³.10 – 2.10³.100/100  ---  N= 20.10³ – 2.10³  ---  N=18.10³N   

Ponto B – depressão

A força resultante centrípeta que é sempre dirigida para o centro da circunferência que é para cima, ou seja, F_C=mV²/R    --- 

N – P=mV²/R  ---  N=20.10² + 2.10³  ---  N=22.10³N

Ponto C – horizontal  ---  N=P  ---  N=20.10³N

Observe que N_B>N_C>N_A

15-

01- Falsa – em qualquer movimento circular, uniforme ou não, existe sempre uma força resultante centrípeta.

02- Correta – vide 01

04- Correta, a força resultante centrípeta tem sempre direção radial e sentido para o centro da trajetória.

08-  Correta. Observe nas figuras abaixo que =.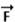

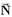Tg45^o=F_C/P  ---  1=F_C/10.000X10   ---   F_C=100.000N

16- F_C=m.V²/R  ---  100.000=10.000.V²/1.000  ---  V=Ö10⁴  ---  V=100X3,6=360km/h.

R: 02 + 04 + 08 + 16=30

16- Para que o astronauta permaneça na mesma posição “colado” à nave, ele deve ter a mesma velocidade angular W que ela e também o mesmo período T (tempo que ela demora para efetuar uma volta completa), que é de 20s.

T=20s  ---  W=2p/T  ---  W=2p/20=p/10  ---  W=p/10rad/s  ---  F_C=m.W².R  ---  F_C=70.(p²/100).10  ---  F_C=7p²N

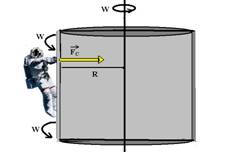
17- a) O “peso” do astronauta é percebido pela reação normal 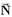 das paredes da nave sobre ele, que é a própria força resultante centrípeta de intensidade N=mV²/R ou N=m.W².R, que nesse caso é seu próprio peso, ou seja, N=P=m.g.

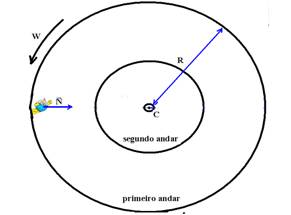
Primeiro andar – raio R  ---  m.g=m.W².R  ---  W=Ö(g/R)

b) ) O “peso” do astronauta é percebido pela reação normal 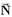 das paredes da nave sobre ele  ---  N=F_C=m.W².(R-h)  --- 

N=m.(Ög/R)².(R-h)  ---  N=m.g.(R-h)/R  ---  Observe na expressão N=m.W².R que se a nave girar com W constante (que é a mesma para todos os andares) e como a massa do astronauta é a mesma, a “gravidade” N é diretamente proporcional ao raio R. Assim, a medida que o astronauta se aproxima do centro C de rotação do sistema a “gravidade” vai diminuindo até se anular no centro C, onde o astronauta tem sensação de ausência de peso (imponderabilidade).

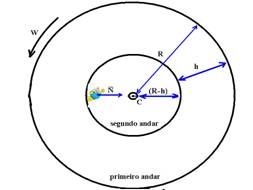
18- a) A velocidade vetorial 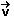tem sempre o sentido do movimento e é sempre tangente à trajetória em cada ponto.

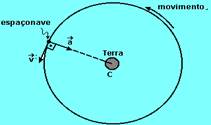
b) Do enunciado F_C=1,5GMm/R², mas sua intensidade também é F_C=mV²/R  ---  m.V²/R=1,5.G.M.m/R²  ---  V=Ö(1,5.G.M)/R

19- a) Como o ponto de entrada do freguês coincide com o ponto de saída, o tempo mínimo de permanência ocorre quando o restaurante efetua um volta completa, o que ocorre no período T  ---  W=2p/T   ---   p/1800=2p/T  ---  T=3.600s ou T=1h

b) F_C=m.W².R=50.( p/1800)².20  ---  F_C=50.(3,14)².20/11(1.800)²  ---  F_C=3.10^-3N

20- a)

b) Somando vetorialmente 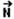com 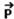 obtemos a força resultante centrípeta 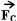, conforme a figura abaixo.

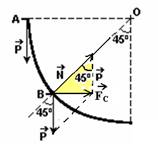
Do triângulo hachurado  ---  tg45^o=F_C/P  ---  1=(m.V²/R)/m.g  ---  V²=R.g  ---  sen45^o=F_C/N  ---  Ö2/2=(m.V²/R)/N  --- 

Ö2/2=m.V²/R.N   ---  Ö2/2=m.R.g./R.N  ---  N=Ö2.m.g

21- a) Tração e peso. A tração sobre o fio no sentido do ponto fixo, enquanto que o peso é vertical para baixo, conforme a figura abaixo.

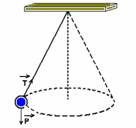
A soma vetorial da força de tração no fio e a força peso nos fornece a força resultante centrípeta.

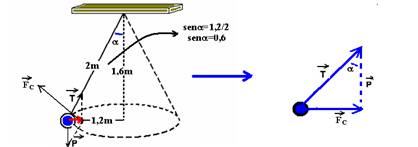
No triângulo da direita  ---  tga=F_C/P=m.V²/m.R.g  ---  1,2/1,6=V²/1,2.10  ---  V=Ö9  --- V=3m/s

sena=F_C/P  ---  0,6=(m.V²/R)/T  ---  0,6= m.V²/R.T  ---  0,6=0,4.9/1,2.T  ---  0,72T=3,6  ---  T=5N

22- O período corresponde ao tempo que ele demora para efetuar uma volta completa  ---  regra de três  ---

60 voltas – 30s

1 volta   -   T

60T=30  ---  T=1/2s  ---  W=2p/T  ---  W=(2p)/1/2  ---  W=4prad/s  ---  Como não há movimento vertical, peso e normal se anulam e, na horizontal a tração no fio é a própria forca resultante centrípeta  ---  F_C­=T=m.W².R=0,5.(4p)².1  ---  T=0,5.16.10.1  --- T=80N  R- B

23- a) 2,0^.10⁴.                    b) 2,6^.10⁴.                      c) 3,0^.10⁴.                     d)2,0^.10³.                     e) 3,0^.10³.

Como ele está em movimento circular existe uma força resultante centrípeta que é sempre dirigida para o centro da circunferência que é para cima, ou seja, F_C=mV²/R  ou  F_C=mW².R  ---  N – P=mV²/R  ou N – P=mW²R.

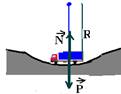
N – 2.10³.10=2.10³.(30)²/3.10²  ---  N=2,6.10⁴N

24- R- B (vide exercício 13)

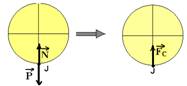
25- Como o movimento é circular e uniforme, a força centrípeta 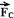= 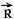e a aceleração centrípeta 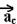= 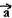 tem a mesma direção

(radial) e o mesmo sentido (para o centro da circunferência) e ambas são sempre perpendiculares ao vetor velocidade 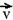, que é sempre tangente à trajetória em cada ponto e tem o sentido do movimento. R- D

26- Nesse caso, a força centrípeta é o F_at que evita com que ele escorregue e saia pela tangente. A força de atrito estático será máxima quando o carro estiver na iminência  de escorregar para fora da pista e nesse caso F_atemáximo=m_eN=m_eP=m_emg  ---  F_c=F_atmáx  ---  mV²/R=m_emg  ---  , que é a máxima velocidade com que ele consegue fazer a curva sem derrapar e,

nesse caso, o coeficiente de atrito deve ser mínimo  ---  20=Öm_e.100.10  ---  400=1.000.m_e  --- m_e=0,4  R- E 

27- Colocando as forças:

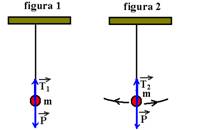
figura 1 – repouso – F_R=0  ---  T₁=P    ---    figura 2 – F_C=T₂ – P  ---  T₂ – P = m.V²/R  ---  T₂=P + m.V²/R  ---  T₂>T₁

28- A velocidade mínima para que o sistema não caia ocorrerá quando a compressão no ponto A for nula, ou seja, quando N=0  ---  F_C=P + N  ---  F_C=P + 0  ---  F_C=P  ---  m.V²/R=m.g  ---  V=ÖR.g  ---  velocidade mínima do sistema (moto + motociclista) no ponto mais alto para fazer a curva e não perder contato com a superfície interna do globo, ou seja, não cair.

V=Ö4,9.10  ---  V=7m/s  R- C

29- No ponto mais alto do morro as forças que agem sobre os dois carros são o peso 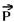 e a força de contato com o solo .

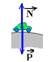
Na iminência de perder contato com o solo, N=0  ---  F_C=P – N  ---  P – N=m.V²/R  ---  P – 0=m.V²/R  ---  mg=mV²/R  ---

V=ÖR.g  ---  verifique pela fórmula que essa velocidade não depende da massa  ---  R- D

30- R- C (veja exercício 27)

31- a e b) Observe a figura abaixo  ---  T – intensidade da força de tração no fio  ---  P – intensidade do peso do acrobata  ---  F_C

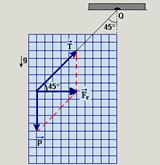
  – intensidade da força resultante centrípeta  ---  sen45^o=P/T  ---  Tsen45^o=P  ---  T.√2/2=mg  ---  cos45^o=F_c/T  ---  F_c=Tcos45^o  --- mV²/R=T.√2/2  ---  mg=mV²/R   ---  V²/R=g  ---  V=√Rg=√4,9.10  ---  V=7m/s  ---  uma volta completa com velocidade de 7m/s  ---  V=ΔS/T  ---  7=2πR/T  ---  7=2.3,14.4,9/T  ---  T≈4,4s

c) Sabemos que T.cos45° = m.g  ---  T.√2/2 = 60.10  ---  T.0,71 = 600  ---   T ≈845 N

Nas condições do teste de segurança  ---  3.T = M_o.g  ---  M_o = 3.845/10  ---  M_o ≈253,5 kg 

32-  Observe a a figura da direita abaixo  ---  R=4 + 10senθ=4 + 10.1/2  ---  R=9m

 Observe a figura da esquerda acima  ---  na vertical  ---  Tcosθ=Mg  ---  Tcos30^o=1000.10  ---  T=10.000/0.87  ---  T=11.494N

A força resultante centrípeta F_R, horizontal, é a componente Tsen30^o  ---  F_R=F_c=Tsen30^o=11.494.1/2  ---  F_c=5.747N 
33- O chamado estado de imponderabilidade ocorre exatamente porque todos os corpos dentro da estação espacial e a própria estação espacial estão sujeitos a mesma aceleração  ---  o que valida a alternativa A  ---  como existe aceleração (gravitacional) da Terra sobre a estação e tudo mais que ela contém, o astronauta possui peso, o que invalida a alternativa B  ---  alternativa c, absurda  ---   o estado do astronauta, bem como de tudo mais da estação não é inercial, pois, como já dito, existe aceleração sobre os corpos em órbita  ---  a velocidade do astronauta pode até ser momentaneamente maior ou menor que a velocidade da própria estação, se ele se desloca dentro dela. Como ele flutua, no mesmo local da estação, subentende-se que a velocidade dele é a da estação, o que invalida a alternativa E.

R- A 

34- O objeto solto bem como o próprio satélite está sujeito à força gravitacional terrestre e logo ambos têm peso  ---  admitindo que o movimento do satélite e do corpo são circulares e uniformes, a aceleração centrípeta será a aceleração gravitacional  ---  a alternativa c é falsa, pois se uma pessoa estiver solta dentro da nave ela não experimenta sensação de peso.

R- B 

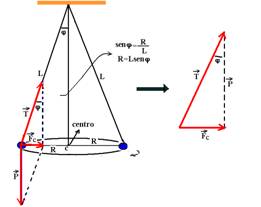
35- Conforme o diagrama anexo, as forças que agem no carro são o peso 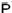 e a normal 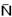. Como o movimento é circular e uniforme, a resultante dessas forças é centrípeta (radial), .

             

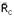tga = R_c/P=ma_c/mg  ---  a_c=gtgα  ---  como a e g são constantes, a aceleração centrípeta (radial, dirigida para o centro) tem módulo constante. 

R- D

36- As forças que atuam sobre o (automóvel + motorista) estão indicadas na figura  ---  a força resultante centrípeta é vertical e para

cima, pois é dirigida para o centro da circunferência  e tem intensidade F_c=mV²/R  ---  N – P=mV²/R  ---  N=860.10 + 860.(20)²/20  ---  N=25.800N  ---  R- D

37- O enunciado sugere tratar-se de um pêndulo cônico ou pêndulo composto  ---  as figuras abaixo ilustram a situação descrita  --- 

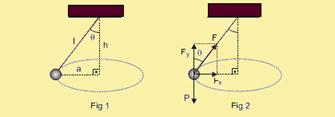
Na Fig 1  ---  h²  +  a²  = l²  ---  h² = l² – a²  ---  h =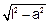 (I)  ---  senθ=a/l  ---  cosθ=h/l  ---  na Fig 2  ---  a componente horizontal da tração (F_x) é a resultante centrípeta (F_c)  ---  F_x = F_c  ---  F sen q = mV²/a  ---  F.(a/l)=mV²/a  ---   F =mV²l/a²(II)  ---  como o movimento se dá num plano horizontal, a resultante das forças verticais é nula  ---  assim, a componente vertical da tração (F_y) equilibra o peso da esfera pendular (P)  ---  F_y = P  ---   F cos q = m g  ---  F.(h/l) = m g  ---  F = mgl/h(III)  ---  igualando (II) e (III)  ---  mV²l/a²=mgl/h  ---  V²=a²g/h (IV)  ---  operíodo (T) é o intervalo de tempo gasto em cada volta (DS = 2pR=2πa)  ---   

v = ΔS/Δt=2πa /T (V)  ---  substituindo (V) em (IV)  ---  (2πa/T)²=a²g/h  ---  4π²a²/T²=a²g/h  ---  T²=4π²h/g  ---  T=2π√h/g (VI)  -

38- Observe a figura abaixo que mostra as forças que agem sobre a pessoa: 

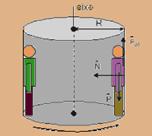
01) Correta  ---   força normal 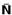 é sempre perpendicular a superfície de apoio, conforme ilustra a figura acima. Nesse caso ela é dirigida para o centro, portanto é uma força centrípeta.
02) Falsa  ---  como a pessoa efetua movimento circular uniforme, na direção horizontal a normal age como resultante centrípeta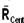  e, na direção vertical, a força de atrito  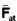deve equilibrar o peso. O piso somente deve ser retirado quando a força de atrito estática máxima for maior ou igual ao peso, caso contrário a pessoa escorrega pelas paredes  ---  N=mV²/R  ---  F_at ³ P  ---  m N ³ m g  ---  inserindo nessa expressão a expressão anterior  ---  μmV²/R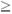mg  ---  μ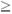Rg/V²  ---  V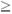√(Rg)/μ  ---  nessa expressão, vemos que a massa da pessoa não interfere e que a velocidade mínima com que o piso pode ser  retirado depende apenas do raio do rotor da intensidade do campo gravitacional local e do coeficiente de atrito entre as roupas da pessoa e a parede do rotor.

04) Verdadeira  ---  conforme demonstração no item anterior.

08) Falsa  ---  o coeficiente de atrito depende apenas das características das superfícies em contato.

16) Falsa  ---  conforme justificativa do item anterior.

R-(01 + 04) = 05

39- Dados  ---   v = 216 km/h = 60 m/s  ---   m = 6 kg  ---   r = 72 m  ---  a força que o piloto deve exercer sobre o conjunto cabeça-capacete é a resultante centrípeta  ---  F_c=mV²/R=6.(60)²/72  ---  F_c=300N  ---  para que um corpo tenha esse mesmo peso, quando sujeito à gravidade terrestre, sua massa deve ser  ---  P/g=300/10  ---  m=30kg  ---  R- B

40-  Dados  ---  h = 2 m  ---   g = 9,8 m/s²  ---   D_ac = 1% g = g/100=0,098 m/s²  ---  um habitante no interior da nave gira com a mesma velocidade angular (w) que ela  ---    diferença entre as acelerações centrípetas nos pés 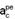 e na cabeça 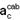deve ser igual a 1% da aceleração da gravidade na Terra.

Pés  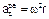---  = g  ---  cabeça  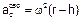---  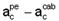  ---  =g/10  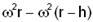---  =g/10  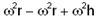---  =g/10  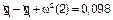---    ---  w² = 0,049  ---  w²r = g  ---  0,049 r = 9,8  ---   r = 9,8/0.049  ---  r=200m

41- Dados  ---  v_o = 0  ---   m = 1.000 kg  ---   H = 30 m  ---   d = 20 m  ---  r = 10 m  ---  observe a figura abaixo  ---  cálculo da

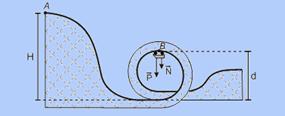
 velocidade no ponto B pela conservação de energia mecânica  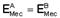---    ---  mgH=mgd + mV²/2  ---  V²=2h(H – d)  --- 

V²=20.(30 – 20)  ---  V²=200  ---  no ponto B, a resultante das forças que agem sobre o carro são radiais, portanto a aceleração é centrípeta  ---  a=a_c=V²/R=200/10  --- a=20m/s²  ---  no ponto B, a resultante é centrípeta e a força vertical que o trilho exerce no carro é a normal 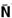  ---  no ponto B a força resultante centrípeta tem direção vertical e sentido para baixo (centro da circunferência)  ---  F_c=N + P=ma  ---  N=ma – mg  ---  N=1.000(20 – 10)  ---  N=10.000N

42- No ponto mais alto quando N=0  ---  F_c=mV²/R  ---  N + P=mV²/R  ---  0 + mg=mV²/R  ---  V=√rg  ---  a_c=V²/r=rg/r  ---  a_c=g  ---  R- E

43- 01. Falsa  ---  a intensidade da força de tensão em C é maior que o peso  ---  existe uma resultante centrípeta vertical e para cima.

02- Correta  ---  veja teoria

04- Falsa  ---  veja 08

08- a menor velocidade e a menor energia cinética ocorre quando a tensão T é nula  ---  T + P=mV²/R  ---  mg=mV²/R  ---  V=√Rg  ---  V=√1.10  ---  V=√10m/s  ---  E_c=mV²/2=0,5.10/2  ---  E_c=2,5J

16- Falsa  ---  T + mg=mV²/R  ---  T=0,5.10 + 0,5.900/2  ---  T=225N

32- Falsa  ---  F_R=F_c=mV²/R=0,5.900/1  ---  F_R=450N

R- (2 + 8)=10

44- A aceleração centrípeta é dada pela expressão a_cp = v²/R. Substituindo os valores para a velocidade de módulo constante do carro, v = 10 km/h, e para o raio da circunferência, R = 5 m = 0,005 km, obtém-se que a_cp = 20.000 km/h².

R- E

45- W=4.360/2  ---  W=720 ^o/s  ---  R- B

46-

Leia atentamente as informações a seguir:

Carro em pista sobrelevada de ângulo θ com a horizontal, sem atrito em pista circular de raio R, contida num plano horizontal.

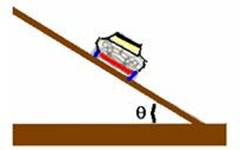
As duas forças que agem sobre o carro, independente do atrito são seu peso 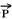 e a reação do solo 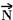. Para que o carro complete a curva a força resultante centrípeta  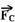 deve ser a soma vetorial de  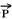com 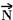 e deve ser radial e dirigida para o centro C  da pista circular de raio R (veja figura abaixo).

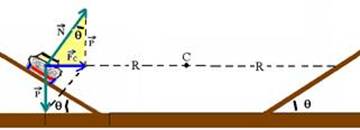
No triângulo hachurado  ---  tgθ=cateto oposto/cateto adjacente  ---  tgθ=F_c/P  ---  tgθ=(mV²/R)/mg  ---  V²=R.g.tgθ

velocidade que o carro deve ter para efetuar a curva sem atrito (ou que seus pneus percam contato (atrito) com a pista).

 V=√(R.g.tgθ)  ---  V²=R.g.tg30^o  ---  100²=R.10.0,58  ---  R=10000/5,8  ---  R=1724,14m  ---  R- D.

 47-

 a) Correta  ---  a_c=V²/R  ---  observe que a aceleração centrípeta é inversamente proporcional ao raio da pista  ---  menor raio, maior aceleração centrípeta.

b) Falsa  ---  W=V/R  ---  a velocidade angular depende do raio da pista.

c) Falsa  ---  A só poderia acompanhar B se eles tivessem a mesma velocidade angular (W=∆θ/∆t), ou seja, eles devem “varrer” o mesmo ângulo no mesmo tempo.

d) e e) Falsas  ---  analise a expressão da força centrípeta  ---  F_c=m.V²/R.

R- A

48-

  Em todo movimento circular existe sempre uma força resultante com direção radial e sentido dirigido para o centro da circunferência, de intensidade F_c=mV²/R, denominada força resultante centrípeta  ---  R- C