Cinemática Vetorial (atividades)

Exercícios resolvidos de Cinemática Vetorial

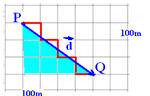
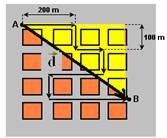
Atividades: ( respostas comentadas no final).
01-(PUCCAMP-SP) Num bairro onde todos os quarteirões são quadrados e as ruas paralelas distam 100m uma da outra, um transeunte faz o percurso de P a Q pela trajetória representada no esquema

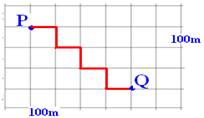
O deslocamento vetorial desse transeunte tem módulo, e metros, igual a:

a) 300                    b) 350                    c) 400                     d) 500                     e) 700

02-(UFB) Um móvel percorre metade de uma circunferência de raio R=5m. Determine:

a) A intensidade de seu deslocamento vetorial e de seu deslocamento escalar (distância percorrida sobre a circunferência)

 03-(PUC-MG) Você e seu amigo resolvem ir ao último andar de um edifício. Vocês partem juntos do primeiro andar. Entretanto, você vai pelas escadas e seu amigo, pelo elevador.

Depois de se encontrarem na porta do elevador, descem juntos pelo elevador até o primeiro andar. É correto afirmar que:

a) o seu deslocamento foi maior que o de seu amigo      b) o deslocamento foi igual para você e para seu amigo      c) o deslocamento de4 seu amigo foi maior que o seu      d) a distância que seu amigo percorreu foi maior que a sua

04-(UFB) A fada Sininho, personagem do famoso filme de Walt Disney, Peter Pan, baseado no livro “Peter and Wendy” de J. M.

Barrie, está voando e descrevendo três quartos de uma circunferência de raio 4m, do ponto P até o ponto Q, no sentido horário, em 2 s. Pede-se determinar, nesse deslocamento:

a) a variação de espaço

b) o vetor deslocamento

c) a velocidade escalar média

d) a velocidade vetorial média

05-(UCBA) Uma partícula percorre a trajetória MNPQ, representada na figura abaixo.

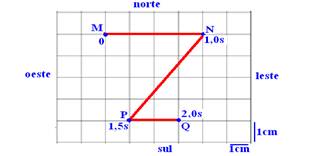
Os instantes de passagem pelos diferentes pontos estão anotados na figura. Determine, nesses 2s, em cm/s:

a) a velocidade escalar média da partícula

b) a velocidade vetorial média  da partícula

06-(UNESP-SP) Nas provas dos 200 m rasos, no atletismo, os atletas partem de marcas localizadas em posições diferentes na

parte curva da pista e não podem sair de suas raias até a linha de chegada. Dessa forma, podemos afirmar que, durante a prova, para todos os atletas, o
a) espaço percorrido é o mesmo, mas o deslocamento e a velocidade vetorial média são diferentes.
b) espaço percorrido e o deslocamento são os mesmos, mas a velocidade vetorial média é diferente.
c) deslocamento é o mesmo, mas o espaço percorrido e a velocidade vetorial média são diferentes.
d) deslocamento e a velocidade vetorial média são iguais, mas o espaço percorrido é diferente.
e) espaço percorrido, o deslocamento e a velocidade vetorial média são iguais.

07-(UERJ) A velocidade vetorial média de um carro de fórmula 1, em uma volta completa do circuito, corresponde a:

(a) 0                (b) 150                  (c) 300                     (d) 600                     e) 700

08-(MACKENZIE-SP) Um corpo é atirado verticalmente para cima a partir do solo com velocidade inicial de módulo 50 m/s. O módulo de sua velocidade vetorial média entre o instante de lançamento e o instante em que retorna ao solo é:

a) 50 m/s                   b) 25 m/s                     c) 5,0 m/s                     d) 2,5 m/s                      e) zero

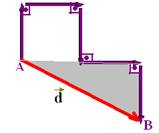
09- (PUC-PR) Um ônibus percorre em 30 minutos as ruas de um bairro, de A até B, como mostra a figura:

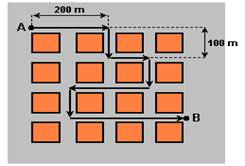
Considerando a distância entre duas ruas paralelas consecutivas igual a 100 m, analise as afirmações:

I. A velocidade vetorial média nesse percurso tem módulo 1 km/h.

II. O ônibus percorre 1500 m entre os pontos A e B.

III. O módulo do vetor deslocamento é 500 m.

IV. A velocidade vetorial média do ônibus entre A e B tem módulo 3 km/h.

Estão corretas:

a) I e III.                     b) I e IV.                       c) III e IV.                     d) I e II.                      e) II e III.

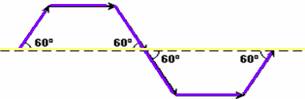
10-(CFT-CE) Uma partícula desloca-se sobre a trajetória formada pelas setas que possuem o mesmo comprimento L. A razão entre a velocidade escalar média e a velocidade vetorial média é:

a) 1/3               b) 2/3                    c) 1                    d) 3/2                     e) 2

11-(PUC-SP) Se a velocidade vetorial de um ponto material é constante e não nula, sua trajetória:

a) é uma parábola      b) pode ser retilínea, mas não necessariamente      c) deve ser retilínea      d) é uma circunferência      e) pode ser uma curva qualquer

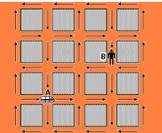
12-. (Unicamp-SP) A figura a seguir representa um mapa da cidade de Vectoria o qual indica a orientação das mãos do tráfego.

Devido ao congestionamento, os veículos trafegam com velocidade escalar média de 18 km/h. Cada quadra desta cidade mede 200 m por 200 m (do centro de uma rua ao centro da outra rua). Uma ambulância localizada em A precisa pegar um doente localizado bem no meio da quadra em B, sem andar na contramão.

a) Qual o menor tempo gasto (em minutos) no percurso de A para B?
b) Qual é o módulo do vetor velocidade média (em km/h) entre os pontos A e B?

13-(UFRN)A figura abaixo representa o deslocamento de um móvel em várias etapas. Cada vetor tem módulo igual a 20m.

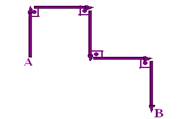
 A distância percorrida pelo móvel e a intensidade do vetor deslocamento são, respectivamente:

a) 20√5m e 20√5m      b) 40m e 40√5m      c) 100m e 20√5m      d) 20√5m e 40m      e) 100m e 40√5m

14-(UFPI) Na figura a seguir, A e B são cidades, situadas numa planície e ligadas por cinco diferentes caminhos, numerados de 1 a 5.

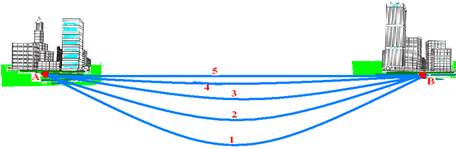
 Cinco atletas corredores, também numerados de 1 a 5, partem de A para B, cada um seguindo o caminho correspondente a seu próprio número. Todos os atletas completam o percurso em um mesmo tempo.

Identifique a opção correta:

a) Todos os atletas foram, em média, igualmente rápidos.

b) O atleta de número 5 foi o mais rápido.

c) O vetor velocidade média foi o mesmo para todos os atletas.

d) O módulo do vetor velocidade média variou, em ordem decrescente, entre o atleta 1 e o atleta 5.

e) O módulo do vetor velocidade média variou, em ordem crescente, entre o atleta 1 e o atleta 5.

15-(UEPG-PR) Pode-se considerar a velocidade pelo aspecto vetorial e escalar. Com relação à velocidade vetorial, quando o

corpo descreve uma trajetória qualquer, assinale o que for correto e dê como resultado a soma dos números correspondentes:

(01) Em qualquer ponto da trajetória, a soma de suas componentes é constante se o movimento for uniforme

(2) A direção é sempre tangente à trajetória

(04) è plenamente determinada quando se conhece seu módulo, sua direção e seu sentido. 

(08) Num ponto da trajetória, o módulo da velocidade vetorial é igual ao valor da velocidade vetorial.

(16) Sendo suas componentes constantes, o movimento é circular e uniforme

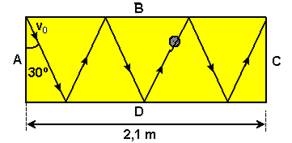
16-(UFPE-PE) Um disco de plástico é lançado com velocidade inicial V_o = 14 m/s fazendo um ângulo de 30° com a borda A de uma mesa horizontal, como mostrado na figura. Após o lançamento, o disco desliza sem atrito e segue uma trajetória em ziguezague, colidindo com as bordas B e D.

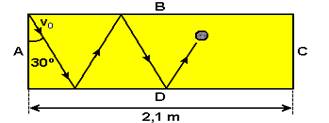
Considerando que todas as colisões são perfeitamente elásticas, calcule o intervalo de tempo, em unidades de 10^-2 segundos, para o disco atingir a borda C pela primeira vez.

17-(UFB) Quando um carro executa uma curva, com velocidade constante, ele está acelerado?

Justifique.

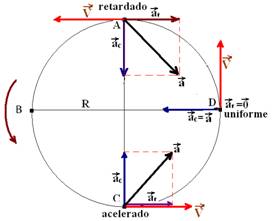
18-(UFB) Um móvel se desloca sobre a trajetória circular da figura no sentido anti-horário. Passa pela primeira vez pelo ponto C em movimento acelerado, pelo ponto D em movimento uniforme, e pelo ponto A em movimento retardado.

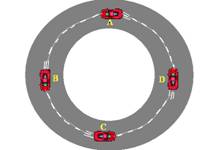
Esboce a velocidade vetorial , a aceleração tangencial (), a aceleração centrípeta (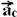) e a aceleração resultante () do móvel, quando passar  pelos pontos C, D e A.

19-(PUC-MG) Um objeto em movimento circular uniforme passa pelo ponto A e, 1s após passa pelo ponto B. A aceleração média

nesse intervalo de tempo é, em m/s²:

a) √2                        b) 2                         c) 0                      d) 0,5                      e) 4

20-(UFU-MG) As informações do movimento de um móvel:

I- A aceleração tangencial é nula

II- A intensidade da aceleração centrípeta é constante e não nula

Por isso, pode-se afirmar que:

a) a direção da velocidade é constante      b) o movimento é retilíneo e uniforme      c) o movimento é circular e uniforme

d) a intensidade da velocidade não é constante      e) o módulo e a direção da velocidade não são constantes

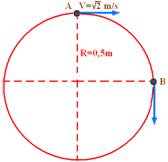
21-(UNIFESP-SP) Um móvel executa um movimento com velocidade escalar constante, ao longo de uma trajetória plana composta de trechos retilíneos e trechos em arcos de circunferências, conforme a figura abaixo.

Os raios de curvatura dos pontos A, B, C, D e E estão indicados na figura.

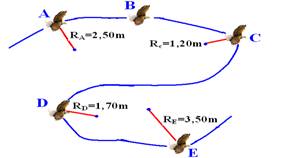
Pode-se afirmar, corretamente, que o módulo máximo da aceleração ocorreu quando o móvel passava nas proximidades do ponto:

a) A                    b) B                       c) C                          d) D                         e) E

22-(FUVEST-SP) Uma partícula tem movimento circular uniforme. Podemos afirmar que:

a) a aceleração vetorial é constante      b) o módulo da velocidade vetorial é constante      c) o módulo da aceleração vetorial é nulo

d) a velocidade vetorial é constante      e) a velocidade vetorial tem seu sentido para o centro da trajetória

23-(FUVEST-SP) Um automóvel executa uma volta completa em uma pista circular, em dois minutos, mantendo constante a

indicação do velocímetro. Em um dos pontos da trajetória, a aceleração vetorial do automóvel te módulo igual a 4m/s². O raio da pista é:

a) zero                    b) 500m                    c) 1.000m                     d) 1.500m                      e) 3.000m

24-(UFPR-PR) Quatro bolas de futebol, com raios e massas iguais, foram lançadas verticalmente para cima, a partir do piso de um ginásio, em instantes diferentes. Após um intervalo de tempo, quando as bolas ocupavam a mesma altura, elas foram fotografadas e tiveram seus vetores velocidade identificados conforme a figura a seguir:

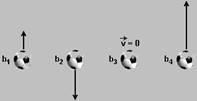
Desprezando a resistência do ar, considere as seguintes afirmativas:

I. No instante indicado na figura, a força sobre a bola b₁ é maior que a força sobre a bola b₂.

II. É possível afirmar que b₄ é a bola que atingirá a maior altura a partir do solo.

III. Todas as bolas estão igualmente aceleradas para baixo.

Assinale a alternativa correta.

a) Somente a afirmativa I é verdadeira.        b) Somente a afirmativa II é verdadeira.        c) Somente a afirmativa III é verdadeira.

d) Somente as afirmativas II e III são verdadeiras.          e) Somente as afirmativas I e III são verdadeiras.

25-(ITA-SP) A figura mostra uma pista de corrida A B C D E F, com seus trechos retilíneos e circulares percorridos por um atleta

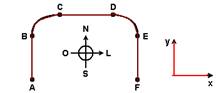
 desde o ponto A, de onde parte do repouso, até a chegada em F, onde pára. Os trechos BC, CD e DE são percorridos com a mesma velocidade de módulo constante.

Considere as seguintes afirmações:

I. O movimento do atleta é acelerado nos trechos AB, BC, DE e EF.

II. O sentido da aceleração vetorial média do movimento do atleta é o mesmo nos trechos AB e EF.

III. O sentido da aceleração vetorial média do movimento do atleta é para sudeste no trecho BC, e, para sudoeste, no DE.

Então, está(ão) correta(s)

a) apenas a I.          b) apenas a I e ll.           c) apenas a I e III.          d) apenas a ll e III.             e) todas.

26-(UFRGS) Um automóvel Z se desloca para a direita mantendo a velocidade de 60km/h ao longo da trajetória mostrada na
figura:

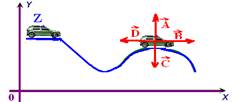
Considerando que esse movimento ocorre numa superfície plana horizontal representada pelo plano desta página(xy), identifique os vetores que melhor indicam a direção e o sentido da velocidade do automóvel e a aceleração centrípeta que atua nele ao passar

pelo ponto P.

 (PUC-SP) Este enunciado refere-se às questões de números 27 e 28. Um móvel parte do repouso e percorre uma trajetória circular de raio 100m, assumindo movimento uniformemente acelerado de aceleração escalar 1,0m/s².

27-(PUC-SP) As componentes tangencial e normal da aceleração valem, respectivamente, após 10s:

a) 1m/s² e zero          b) 10m/s² e 1m/s²          c) 10m/s² e 1om/s²          d) 10m/s² e 100m/s²             e) 1m/s² e 1m/s²        

28-(PUC-SP) O ângulo formado entre a aceleração total e o raio da trajetória no instante t=10s vale:

a) 180^o                 b) 90^o                   c) 60^o                  d) 45^o                   e) 30^o

29-UFPA) Uma partícula percorre, com movimento uniforme, uma trajetória não retilínea. Em cada instante teremos que:

a) Os vetores velocidade e aceleração são paralelos entre si;          b) A velocidade vetorial é nula;

c) Os vetores velocidade e aceleração são perpendiculares entre si;      d) Os vetores velocidade a aceleração têm direções independentes;      e) O valor do ângulo entre o vetor velocidade e o vetor aceleração muda de ponto a ponto.

30-(Ufla-MG) Uma criança brinca com um rotor de um playground, conforme a figura, que está realizando movimento circular e uniforme com velocidade em módulo de √2m/s.

  

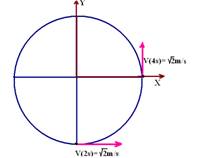
Entre os instantes t=2s e t’=4s, o módulo da aceleração média será de :

a) 0               b) -1m/s²                     c) 1m/s²                    d) √2m/s²                    e) √2/2m/s²

31-(UNESP-SP) Suponha que um professor de Física esteja em repouso no compartimento de um trem, sem contato visual com o

 

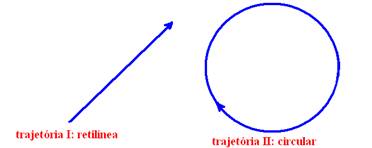
exterior e que o trem se mova seguindo uma das trajetórias indicadas na figura.

Se o trem se movesse com velocidade V constante, esse professor detectaria o movimento do trem em relação à Terra:

a) apenas para o caso da trajetória I          b) apenas para o caso da trajetória II          c) para ambas as trajetórias

d) para ambas as trajetórias, se V fosse próxima à velocidade da luz          e) para nenhuma das trajetórias

32-(UFCE-CE) Uma partícula descreve trajetória circular, de raio r=1,0m, com velocidade variável. A figura mostra a partícula em um dado instante de tempo em que sua aceleração tem módulo a=32m/s² e aponta na direção e sentido indicados.

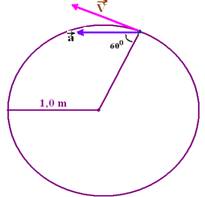
Nesse instante, o módulo da velocidade da partícula é:

a) 2,0m/s                  b) 4,0m/s                   c) 6,0m/s                  d) 8,0m/s                e) 10,0m/s

33-(UFMG-MG) Um ventilador acaba de ser desligado e está parando vagarosamente, girando no sentido horário.

A direção e o sentido da aceleração da pá do ventilador no ponto P é:

34-(UEPB) (UEPB) De acordo com os conceitos estudados em Cinemática, complete adequadamente a coluna da direita com os itens da esquerda:

(1) Movimento retilíneo e uniforme.   ( ) Velocidade vetorial de direção constante e módulo variável.

2) Movimento retilíneo e uniformemente variado. ( ) Velocidade vetorial constante.

(3) Movimento circular e uniforme.    ( ) Velocidade vetorial variável em direção e módulo.

(4) Movimento circular e uniformemente variado. ( ) Velocidade vetorial de módulo constante e direção variável.

Assinale a alternativa que corresponde à seqüência correta da numeração:

a) 1, 2, 3, 4.                b) 2, 1, 4, 3.                   c) 3, 4, 1, 2.                  d) 1, 3, 4, 2.                  e) 3, 4, 2, 1.

35-(FGV-SP) A figura que melhor representa os vetores velocidade instantânea e aceleração instantânea , para uma partícula descrevendo um movimento circular uniforme é:

36-(UFSCAR-SP) Nos esquemas estão representadas a velocidade e a aceleração do ponto material P. Assinale a alternativa em que o módulo da velocidade desse ponto material permanece constante.

37-(FATEC-SP) Num certo instante estão representadas a aceleração e a velocidade vetoriais de uma partícula. Os módulos dessas grandezas estão também indicados na figura. Dados: sen60^o=0,87         cos60^o=0,50

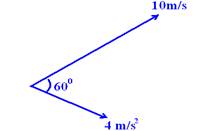
No instante considerado , o módulo da aceleração escalar, em m/s², e o raio de curvatura, em metros, são, respectivamente,

a) 3,5 e 2,5                b) 2,0 e 2,8                 c) 4,0 e 36                 d) 2,0 e 29                 e) 4,0 e 58

38- (Uniube-MG) A figura a seguir representa um pêndulo simples que oscila entre as posições A e B, no campo gravitacional terrestre. Quando o pêndulo se encontra na posição P, a sua aceleração resultante é melhor indicada pelo vetor:

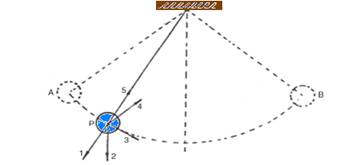
a) 1.                    b) 2.                  c) 3.                   d) 4.               e) 5.

39-(UECE-CE-2009) Uma partícula puntiforme tem, em certo instante t, a velocidade, em m/s, dada por v_o = 1,0 i - 2,0 j + 5,0 k. Dois segundos depois, sua velocidade, em m/s, é dada por v = 4,0 i - 2,0 j + 1,0 k. No intervalo de tempo considerado, o módulo da aceleração média, em m/s², é:

a) 25,0             b) 5,0              c) 1,0               d) 2,5                 e) 4,5

40-(UFG-GO-09) No começo fiquei assustado. Mas talvez não seja especialmente horrível a idéia que li na "Folha" deste domingo, sobre a mais nova profissão do mundo. Trata-se do "personal amigo", e o nome, por si só, já é um poema. Amigos, por definição, sempre serão pessoais; o "personal amigo" inverte o sentido da expressão. Você paga uma taxa - que vai de R$ 50 a R$ 300, imagino que de acordo com a qualidade do profissional - e fica com uma pessoa para conversar, ir com você ao shopping ou

tomar uma água de coco durante sua caminhada. Seria fácil pôr as mãos na cabeça e ver nessa novidade mais um sintoma da extrema mercantilização da vida cotidiana dentro dos quadros do capitalismo avançado. Creio que não se trata disso. Ninguém confundirá "personal amigo" com um amigo de verdade. Namoro, amizade, relacionamento? Acho bom que a extrema variação das emoções humanas não fique limitada a duas ou três palavras. Mandaram-me a notícia de que um site de livros eletrônicos entrega pelo correio uma fita adesiva para grudar no computador. A fita tem cheiro de livro real. Eis aí, quem sabe, o segredo do "personal-qualquer coisa". Ficamos muito tempo navegando no mundo virtual. Há o medo e a necessidade de entrar em contato físico com a realidade. Contrata-se um "personal amigo": pode ser um amigo falso, mas é uma pessoa real. A solidão pode ser driblada nas conversas pela internet. Mas não é apenas distração e conversa o que se procura: há, como nos adesivos com cheiro de livro verdadeiro, necessidade de coisa mais profunda, quem sabe até se religiosa; penso em termos como presença, calor, vida e comunhão.

            COELHO, Marcelo. "Do virtual ao personal". Folha de S. Paulo, São Paulo, 29 ago. 2007, p. E9. [Adaptado].

O excesso de navegação no mundo virtual fez com que um cidadão (CI), "ao se sentir obeso", procurasse um contato físico com a realidade e, para tal, contratou um personal amigo (PA) para fazer parte de seus exercícios matinais. Suponha que isso tenha ocorrido em uma praça quadrada de Goiânia, de lado 300 m, conforme a figura a seguir.

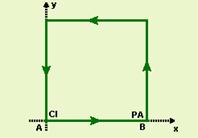
Previamente combinado, as duas pessoas, CI e PA, saíram no mesmo instante de suas posições iniciais, A e B, representadas na figura, caminhando no sentido anti-horário. CI partiu do repouso com aceleração de 5,0.10^-3 m/s², e PA andou desde o início com velocidade constante de 1,0 m/s. Determine, para a posição em que se encontraram:

a) o vetor velocidade média (módulo, direção e sentido) do PA;

b) a velocidade escalar média do CI.

  

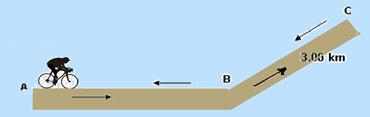
41-(ITA-SP-010) Na figura, um ciclista percorre o trecho AB com velocidade escalar média de 22,5 km/h e, em seguida, o trecho BC de 3,00 km de extensão. No retorno, ao passar em B, verifica ser de 20,0 km/h sua velocidade escalar média no percurso então percorrido, ABCB. Finalmente, ele chega em A perfazendo todo o percurso de ida e volta em 1,00 h, com velocidade escalar média de 24,0 km/h. Assinale o módulo v do vetor velocidade média referente ao percurso ABCB.

 a) v = 12,0 km/h                         b) v = 12,00 km/h                    c) v = 20,0 km/h                            d) v = 20, 00 km/h 

e) v = 36, 0 km/h 

 

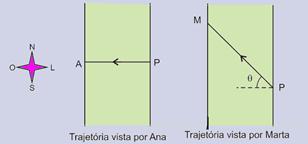
42-(FUVEST-SP-010)  Pedro atravessa a nado, com velocidade constante, um rio de 60 m de largura e margens paralelas, em 2

minutos. Ana, que bóia no rio e está parada em relação à água, observa Pedro, nadando no sentido leste-oeste, em uma trajetória retilínea, perpendicular às margens. Marta, sentada na margem do rio, vê que Pedro se move no sentido nordeste-sudoeste, em uma trajetória que forma um ângulo θ com a linha perpendicular às margens. As trajetórias, como observadas por Ana e por Marta, estão indicadas nas figuras a seguir, respectivamente por PA e PM.

Se o ângulo θ for tal que cos θ = 3/5(senθ=4/5), qual o valor do módulo da velocidade

a) de Pedro em relação à água?

b) de Pedro em relação à margem?

c) da água em relação à margem?

43-(UFRN-RN-011) Uma característica da profissão de carteiro é que ele anda muito através das ruas, fazendo diversos percursos ao longo do seu dia de trabalho. Considere a situação do mapa representado pela figura abaixo, na qual um carteiro que se encontra no ponto A, localizado na Av. Amintas Barros, se desloca 400m até atingir o cruzamento desta com a Av. Xavier da Silveira,

  

ambas as avenidas situadas em Natal (RN).

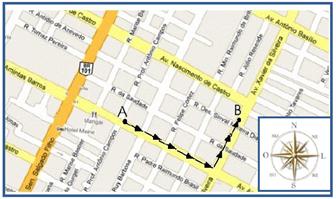
Em seguida, a partir daquele cruzamento, o carteiro se desloca por mais 300m nesta última avenida até chegar ao endereço procurado, localizado no ponto B.

Considerando o percurso e as orientações indicadas no mapa, pode-se afirmar que o módulo, a direção e o sentido do vetor deslocamento do carteiro são, respectivamente,

A) 700m, L-O e para L.           B) 500m, O-L e para O.           C) 500m, O-L e para L.           D) 700m, L-O e para O.

44-(UEPA-PA-011) Ao longo do ano muitos pássaros  migram de seus locais de origem para diferentes regiões  do planeta. Admita que um pássaro migratório se movimente do sul para o norte com velocidade constante de 20km/h, durante 15 minutos, em uma trajetória retilínea. Na seqüência ele muda de direção e percorre 5 km, de tal maneira que sua nova velocidade forma um ângulo de 60^o com a velocidade inicial. O módulo do deslocamento resultante do pássaro, a partir do ponto inicial, em quilômetros, é:

a) 5                             b) 3√5                                  c) 5√2                                d) 5√3                                e) 10   

Resoluções

01- Aplicando Pitágoras no triângulo hachurado  ---  d=500m  ---  R- D

02- a) Supondo que ele se desloque no sentido anti-horário indo de M para N, o deslocamento vetorial  é obtido unindo os pontos M 

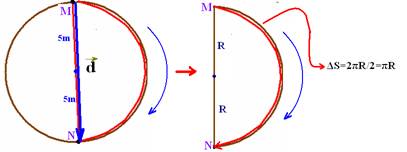
e N e a intensidade do vetor deslocamento é d=2R=2.5  ---  d=10m  ---  ΔS=2πR/2= πR=5π  ---  ΔS=5π m

03- R- B  ---  Quando um corpo sai de um ponto A, desloca-se até um ponto B, e retorna ao ponto A, mesmo que com trajetórias diferentes na ida e na volta, seu deslocamento vetorial  é nulo, pois você está somando e subtraindo dois vetores de mesma direção, mas de sentidos opostos.

04- a) A variação de espaço ΔS representa a distância efetivamente (realmente) percorrida pelo corpo (distância medida sobre a trajetória) durante o percurso de 3/4 da mesma  ---   ΔS=3/4.2πR=3/4.2π.4  ---  ΔS=6π m  

b) O vetor deslocamento é obtido unindo-se os pontos P e Q, com sentido de P para Q

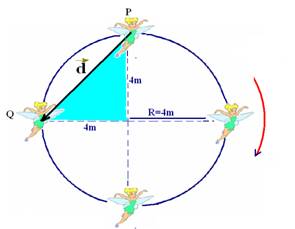
Aplicando Pitágoras no triângulo hachurado  ---  d²=4² + 4²  ---  d=√32  ---  d=4√2 m  ---  direção – oblíqua  ---  sentido - sudoeste

c) V_m= ΔS/Δt=6π/2  ---  V=3πm/s

d) V_m=d/Δt=4√2/2  ---  V_m=2√2 m/s  ---  direção – oblíqua  ---  sentido - sudoeste

05- a) (NP)²=4² + 3²  ---  NP=5cm  ---   ΔS=MN + NP + PQ=4 + 5 + 2  ---   ΔS=11cm  ---  V_m= ΔS/Δt=11/2  ---  V_m=5,5cm/s

b) A velocidade vetorial média 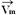 é obtida unindo M com Q e com sentido de M para Q 

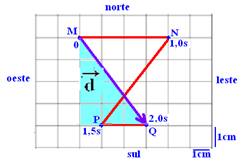
Aplicando Pitágoras no triângulo hachurado  ---  d=5cm  ---  V_m=d/Δt=5/2  --- V_m=2,5cm/s – inclinada - sudeste

06- R- A (veja teoria)

07- Quando um corpo sai de um ponto A, desloca-se até um ponto B, e retorna ao ponto A, mesmo que com trajetórias diferentes na ida e na volta, seu deslocamento vetorial  é nulo, pois você está somando e subtraindo dois vetores de mesma direção, mas de sentidos opostos. Se  é nulo, a velocidade vetorial média também é nula, pois V=d/t  ---  V=0/t  ---  V=0  ---  R- A

08- R- E – veja resolução do exercício anterior

09- I – Observe no triângulo hachurado da figura abaixo que d=300² + 400²  ---  d=500m=0,5km  ---  V_m=d/t=0,5/0,5  ---  V=1km/h -

correta

II- Falsa  ---  a distância percorrida vale ΔS=200 + 100 + 100 + 100 + 200 + 100 + 300  ---  ΔS=1.100m

III- Correta – veja I

R- A

10- velocidade escalar  ---  V_me=ΔS/Δt=6L/t  ---  velocidade vetorial V_mv=d/t  ---  Lcos60^o=L.12=L/2  ---  V_mv=L/2 + L + L/2 + L/2 +

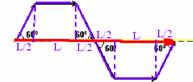
L + L/2=4L  ---  V_mv=4L/t  ---   t é o mesmo  ---  V_me/V_mv=(6L/t)/(4L/t)  --- V_me/V_mv=3/2  ---  R- D

11- Se a velocidade vetorial é constante e não nula, ela tem em todos os pontos a mesma intensidade, mesma direção e mesmo sentido e, nesse caso o movimento só pode ser um  movimento retilíneo e uniforme  ---  R- C

12- a) veja figura abaixo:

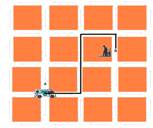
Vm=18km/h=5m/s  ---  menor caminho  ---  ΔS=200 + 400 + 200 + 100 =900m  ---  Vm=ΔS/Δt  ---  5=900/t  ---  t=180s=3minutos

b) A intensidade do vetor deslocamento  é obtida aplicando Pitágoras no triângulo hachurado da figura abaixo  ---  d² = 300² +

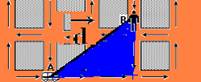
400²  ---  d=500m  ---  o tempo de percurso é o mesmo t=180s  ---  V_mv=d/t=500/180x3,6  ---  V_mv=10km/h  

13- ΔS=20 + 20 + 20 + 20 + 20  ---  ΔS=100m  ---  o deslocamento vetorial  é obtido unindo-se A com B, no sentido de A para B

Aplicando Pitágoras no triângulo hachurado  ---  d²=40² + 20²  ---  d=20√5m  ---  R- C

14- Como os intervalos de tempo são iguais parara todos os atletas e o deslocamento vetorial também é o mesmo (obtido, em cada caso, unindo os pontos A e B), o vetor velocidade média (V_m=d/t), também será o mesmo para todos os atletas  ---  R- C

 15- (01) Falsa, pois se o movimento for circular e uniforme a velocidade vetorial varia em direção e sentido.

(02) Correta – veja figuras abaixo

 

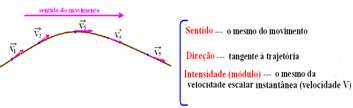
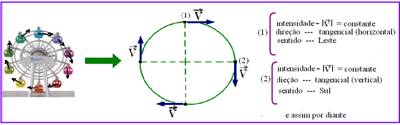
(04) Correta – todo vetor fica determinado quando se conhece sua intensidade, direção e sentido.

(08) Correta – veja (02)

(16) Falsa – veja (01)

R- soma (02 + 04 + 08)=14

16- No triângulo abaixo  ---  sen30^o=cateto oposto/hipotenusa=x/d  ---  1/2 = x/d   ---  x=d/2  --- nessas condições, o triângulo do meio

  

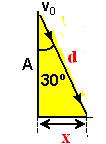
 eqüilátero de lados d  ---  como tem-se 3 triângulos eqüiláteros de lados d  ---  3d=2,1  ---  d=0,7m – observe na figura acima que ele percorre ΔS=6d=6.0,7  ---  ΔS=4,2m  ---  V= ΔS/t  ---  14=4,2/t  ---  t=0,3s  ---  t=30.10^-2s

17- Sim, pois sempre que um corpo efetua uma curva com qualquer velocidade, mesmo constante, surge sobre ele uma força que o obriga a fazer a curva (no caso a força de atrito), que é denominada força resultante centrípeta, de direção radial e dirigida para o centro da curva. Se existe força centrípeta, existirá também aceleração centrípeta também de direção radial e dirigida para o centro da curva.

18- Observe com muita atenção cada caso esquematizado na figura abaixo

19- Como ele está em movimento circular uniforme, a intensidade do vetor velocidade é constante e vale V=√2m/se, então não existe aceleração tangencial, mas somente centrípeta, de intensidade  ---  a_c=V²/R=(√2)²/0,5=2/0,5  ---  a_c=4m/s²  ---  R- E

20- Se a_t=0, o movimento é uniforme e se a_c=constante e não nula ele está em trajetória circular (V e R são constantes). Portanto trata-se de um movimento circular uniforme  ---  R- C

21- Como a velocidade escalar V é constante, não existe a_t, somente a_c que é fornecida por a_c=V²/R  ---  como V é constante, a_c é inversamente proporcional a R, ou seja, menor R – maior a_c  ---  R- C

22- No movimento circular uniforme, movimento em que a intensidade (módulo) da velocidade vetorial é constante, sua direção 

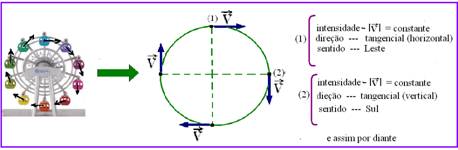
e sentido variam, pois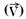é tangente à trajetória em cada ponto.  ---  R- B

23- Se a indicação do velocímetro é constante a aceleração tangencial é nula, restando apenas a aceleração centrípeta (a_c=V²/R)  --- 

1voltas completa  ---  ΔS=2πR ---  Δt=2min=2.60  ---  Δt=120s  ---  V=ΔS/Δt=2πR/120  ---  V=πR/60  ---  a_c=V²/R  ---  4=(πR/60)²/R  ---  4=π²R²/3.600 x 1/R  --- 14.400=π².R  ---  R=14.400/π²=14.400/9,9596=1.445,9m  ---  R- D

24- I- Falsa – como a resistência do ar é desprezada, a força resultante que age sobre cada bola é seu peso (P=mg,vertical e para baixo)

II- Correta – sendo a aceleração tangencial constante (a_t=g), a maior altura será atingida por aquela que tem maior velocidade inicial.

III_ Correta – pela aceleração da gravidade g, vertical e para baixo

R- D

25- I- no trecho AB é acelerado com a_t, pois partiu do repouso V_o=0  ---  nos trechos BC e DE, não tem a_t (velocidade constante) mas tem a_c (trajetória curva)  ---  no trecho EF é retardado com a_t, pois está freando até parar  ---  correta  

II- correta – num trecho ele acelera e no outro, retarda.

III- correta – veja figura abaixo

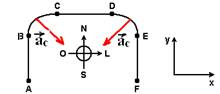
R- E

26- O vetor velocidade é tangente à trajetória e tem o sentido do movimento (horizontal e para a direita)  ---  a aceleração centrípeta é dirigida para o centro da curva (vertical e para baixo)  ---  R- 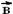e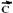

27- De acordo com o enunciado a_t=1m/s²  ---  V após 10s vale V=V_o + at  ---  V= 0 + 1.10  ---  V=10m/s  ---  a_c=V²/R=10²/100  ---  a_c=1m/s²

28- Observe a figura abaixo

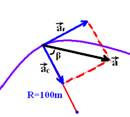
a²=1² + 1²   ---  a=√2m/s²  ---  senβ=a_t/a  ---  senβ=1/√2  ---  senβ=√2/2  ---  β=45^o  ---  R- D

29-  Movimento uniform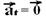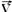e  ---  ---   e 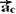 são perpendiculares   ---  R- C

30- Entre 2s e 4s ele percorreu um quarto do arco da circunferência  ---  ΔS=2πR/4  ---  V= ΔS/Δt  ---  √2=(πR/2)/(4-2)  ---  4√2=πR  ---  R=4√2/π  ---  R= 1,8m  ---  sendo a velocidade constante só existe aceleração centrípeta, também constante  ---  a_c=V²/R  --- 

a_c= (√2)²/1,9=1,0m/s²  ---  R- C

31- Somente na trajetória II, onde existe aceleração centrípeta e consequentemente força centrípeta e, pelo princípio da inércia ele se “sentirá jogado”, em sentido contrário ao da curva, tentando sair pela tangente  ---  R- B

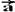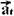32- Na figura abaixo a aceleração  está decomposta em suas parcelas  e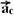

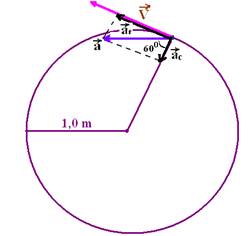
cos60^o=a_c/a  ---  0,5=a_c/32  ---  a_c=16m/s²  ---  a_c=V²/R  ---  16=V²/1  ---  V=4m/s  ---  R- B

33- Veja esquema abaixo:

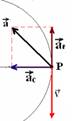    R- D

34- R- B  (veja teoria)

35- Se está em MCU, a aceleração tangencial é nula, a velocidade vetorial é tangente e a aceleração é a centrípeta  ---  R- D

36- R- C  ---  está em movimento circular uniforme

37- A figura abaixo mostra os vetores 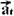 e 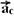, decompostos a partir do vetor .

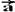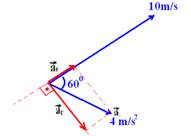
sen60^o=a_c/4  ---  0,87=a_c/4  ---  a_c=3,48m/s²  ---  a_c=V²/R  ---  3,48=(10)²/R  ---  R=29m  ---  cos60^o=a_t/4  ---  0,50=a_t/4  ---  a_t=2,0m/s²  ---  R- D

38-

Veja figura abaixo

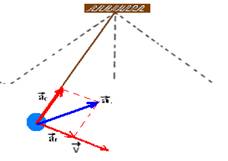
R- D

39- Trata-se de uma localização em três dimensões

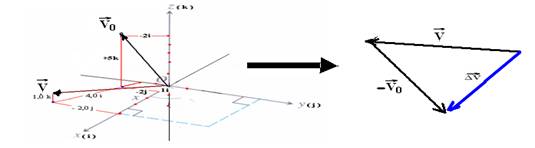
ΔV=V – V₀=(4i – 2j + k) – (i -2j + 5k) = 4i -2j +k –i +2j – 5k  ---  ΔV=3i – 4k  ---  a= ΔV/Δt=(3i – 4k)/2  ---  a=1,5i – 2k

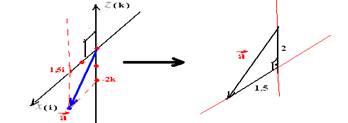
a²=(1,5)² + (2,0)²  ---  a=√6,25  ---  a=2,5m/s²  ---  R- D

40- a) Como CI parte de A e PA parte de B, o deslocamento de CI deve ser 300m maior que o deslocamento de PA  --- ΔS_CI=ΔS_PA +300  ---  como o movimento de CI é uniformemente variado e o de PA é uniforme  ---  equações de cada um com a origem em A  ---  ΔS_CI=gt²/2  ---  ΔS_PA=Vt + 300  ---  no encontro  ---  ΔS_CI=ΔS_PA  ---  5.10^-3t²/2=1.t + 300  ---  2,5.10^-3t² – t + 300=0  ---  resolvendo a equação  ---  t=600s (tempo do encontro)  ---  deslocamento escalar de PA  ---  ΔS_PA=Vt=1.600  ---  ΔS_PA=600m  --- 

como PA percorreu 600m até o encontro, ele ocorre no ponto D da figura abaixo  ---  a diagonal do quadrado (BD) é o

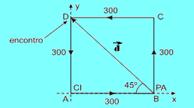
deslocamento vetorial (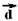) de PA e tem intensidade   ---  d=300√2m  ---  o vetor velocidade média (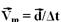) tem intensidade  ---  V_m=300√2/600  ---  V_m ≈ 0,7m/s, direção  ---  oblíqua  ---  sentido  ---   NO formando um ângulo de 45^o com a horizontal.

b) CI andará 900m até o encontro  ---  V_m=900/600  ---  V_m=1,5m/s

             

41- Cálculo do deslocamento em todo o trajeto DS = v.Dt = 24.1 = 24 km  ---  distância AB pode ser calculada da seguinte forma  -- DS = 2.AB + 2.BC  ---  DS/2 = AB + BC  ---  AB = DS/2 – BC =24/2– 3 = 12 – 3 = 9 km  ---   tempo total gasto no trecho ABCB

v = DS/Dt  ---  Dt = DS/v = (9 + 6)/20= 15/20  ---  Dt = 0,75 h  ---   módulo da velocidade vetorial média 9/0,75 = 12 km/h

R- A

42- Dados  ---  largura do rio D = 60 m  ---   Dt = 2 min = 120 s  ---  cos q = 4/5  ---  sen q =3/5  ---  a figura abaixo ilustra as

velocidades, sendo: v a velocidade de Pedro em relação à margem; V_p/ag: a velocidade de Pedro em relação à água e v_ag a velocidade da água.

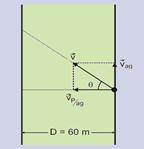
a) V_p/ag=D/Δt=60/120  ---  V_p/ag=0,5m/s 

b) Da figura  ---  cosθ= V_p/ag/V  ---  3/5=0,5/V  ---  V=2,5/3  ---  V=0,83m/s

c) Da mesma figura  ---  senθ=V_ag/V  ---  4/5=V_ag/2,5/3  ---  V_ag=10/15  ---  V_ag=0,67m/s

43- O vetor deslocamento (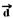) do carteiro é obtido unindo-se os pontos A com B, figura abaixo  ---  o módulo de 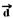 é fornecido pelo teorema de Pitágoras  ---  d²=400² + 300²  ---  d=500m  ---  direção oeste-leste  ---  sentido para o leste  ---  R- C

44- Distância percorrida do sul para o norte  ---  V=ΔS/Δt  ---  20=ΔS/(15/60)  ---  ΔS=5km  ---  o novo deslocamento de 5km forma um ângulo de 60^o com o deslocamento inicial  ---  veja a figura abaixo onde 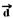 é o vetor deslocamento pedido  ---  aplicando a

                        

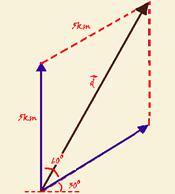
lei dos cossenos  ---  d²=5² + 5²  + 2.5.5.cos60^o  ---  d=√75  ---  d=5√3m